Zwillingsparadoxon - die Berechnungen nach der Lorentz-Transformation
Hier sind die Gleichungen der Lorentztransformation (LT), die als Grundlage der Speziellen Relativitätstheorie dienen, wobei die anderen zwei Raumkoordinaten y = y´ und z = z´ nicht inbegriffen
sind. 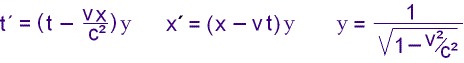
Die Bedeutung der Symbole:
t ist immer die Zeit vor Ort, sowie die zeitliche Koordinate im „ruhenden“ Inertialsystem, auch Eigenzeit genannt
x ist immer die räumliche Koordinate im „ruhenden“ Inertialsystem (IS), delta x wird Eigenlänge genannt.
t´ ist immer die Zeit im „bewegten“ Inertialsystem aus der Sicht der Beobachter im „ruhenden“ IS – ist aber
keine Eigenzeit im „bewegten“ IS
x´ ist immer die räumliche Koordinate im „bewegten“ IS aus der Sicht der Beobachter im „ruhenden“ IS – ist aber
keine Eigenlänge im „bewegten“ IS.
Die gestrichelten Symbole zeigen die Werte, Koordinaten eines Punktereignisses, die nach Meinung der „ruhenden“ Beobachter die „bewegten“ messen müssten, um die Bedingung einer invarianten Lichtgeschwindigkeit erfüllen zu
können.
Nehmen wir als Beispiel die Erde und eine Rakete. Die Erdbeobachter postulieren wir als „ruhend“ und die
Raketenbeobachter als „bewegt“. Die Koordinaten eines Punktereignisses wären dann aus Erdsicht tE und xE. Nach Meinung der Erdbeobachter (auch nach Zweiwegmessung mit Licht oder Funksignalen, wie bereit beschrieben) müssten
die Koordinaten desselben Punktereignisses aus Sicht der Raketenbeobachter t´R und x´R sein.
Werden wir aber jetzt die Rakete als „ruhend“ postulieren und wollen wissen was die jetzt „ruhenden“
Raketenbeobachter vor Ort, d.h. in der Rakete, tatsächlich messen werden, dann lauten die Koordinaten tR und xR – jetzt sind die Symbole ungestrichelt. Nach Meinung der Raketenbeobachter müssten die Koordinaten desselben
Punktereignisses aus Sicht der Erdbeobachter t´E und x´E sein.
Dass die gestrichelten Koordinaten NICHT die EIGENZEIT und EIGENLÄNGE des “bewegten” IS darstellen, wird später aus den Berechnungen ersichtlich und bewiesen.
Was bedeutet „Punktereignis“ – das kann ein Blitzen, eine Licht- oder Funkreflexion, ein Ereignis also, das sich in sehr kurzer Zeit abspielt. Da bei den Betrachtungen nach der Speziellen Relativitätstheorie die Lichtstrahlen immer und nur relativ zum Beobachter sich konstant mit c ausbreiten (gemessen werden), spielt keine Rolle, ob das Objekt, an dem sich das Punktereignis abspielt, bewegt oder unbewegt relativ zum Beobachter wäre. Demzufolge sagt man, ein Punktereignis ist immer unbewegt.
Um nach der Lorentz-Transformation irgendwelche Koordinaten berechnen zu können, müssen wir zuerst bestimmen,
wo das Punkereignis stattfindet, bzw. wenn wir längere Zeiträume und Bewegungen beschreiben wollen, dann wo eine Abfolge aus Punkereignissen sich befindet.
Bei dem bereits behandelten Beispiel in Minkowski-Diagrammen, können wir die Ereignisfolge auf die Erde, auf die
Rakete (Raketen) oder auf den Zielplanet postieren. Bei einer kompletten Betrachtung kann man natĂĽrlich den Ort der
Ereignisfolge nicht wechseln – d.h. wenn der Ort der Ereignisfolge auf der Rakete postiert ist, muss dieser Ort bei Hin- und Rückreise immer dort bleiben. Die Koordinaten tE , xE ; tR , xR und tP , xP sind Koordinaten aus den „unbewegten“
fĂĽr sich Erde, Rakete und Zielplanet.
Die Daten fĂĽr das Beispiel sind wie gehabt: Erde und Zielplanet sind unbewegt zueinander und auf Abstand 3 LJ, auf
dem Zielplanet befinden sich auch Beobachter mit Uhren, die synchron mit den irdischen laufen. Die Rakete fliegt von der Erde zum Zielplanet und zurück mit v = 0,6c. Keine Beschleunigungen werden einbezogen – s. die Konstellation beim Drillingsparadoxon – die Rakete fliegt in Richtung Zielplanet mit 0,6c an die Erde vorbei und dort vor Ort übernimmt (synchronisiert mit) die irdische Zeit – bei der Rückreise genauso, die Rakete (oder eine andere) fliegt jetzt in Richtung Erde mit 0,6c an den Zielplanet vorbei und übernimmt dort vor Ort die Zielplanet-Zeit, die natürlich identisch mit der Erdzeit ist.
c = 1 und v in c-Einheit - so werden die Gleichungen der LT ĂĽbersichtlicher.
y ist bei 0,6c = 1,25. Startzeit t0 = 0h (0J).
1. Postieren wir zuerst die Ereignisfolge auf die Rakete, Punktereignisse jährlich nach Erdzeit, die „unbewegten“ Beobachter sind auf der Erde.
a) Hinreise: x ist positiv, v in Richtung zunehmende x – auch positiv:
Start tE = 0J; xE = 0,0LJ > t´R = (tE – v*xE)*y = (0 – 0,6*0)*1,25 = 0J
tE = 1J ; xE = 0,6LJ > t´R = (tE – v*xE)*y = (1 – 0,6*0,6)*1,25 = 0,8J
tE = 2J ; xE = 1,2LJ > t´R = (tE – v*xE)*y = (2 – 0,6*1,2)*1,25 = 1,6J
tE = 3J ; xE = 1,8LJ > t´R = (tE – v*xE)*y = (3 – 0,6*1,8)*1,25 = 2,4J
tE = 4J ; xE = 2,4LJ > t´R = (tE – v*xE)*y = (4 – 0,6*2,4)*1,25 = 3,2J
tE = 5J ; xE = 3,0LJ > t´R = (tE – v*xE)*y = (5 – 0,6*3,0)*1,25 = 4,0J J
Die räumlichen Koordinaten sind:
Start xE = 0LJ > x´R = (xE – v*tE)*y = (0 – 0,6*0)*1,25 = 0LJ und bleiben während der ganzen Reise = 0, da die
Punktereignisse vor Ort bei der Rakete sind.
Nach Meinung der Erdbeobachter mĂĽsste die Rakete bei Erdzeit = 5J den Zielplanet erreicht haben, die Raketenuhren mĂĽssten aber eine Zeit = 4J zeigen. Diese und nur diese Konstellation des Ereignisortes verleitet naive Betrachter an
eine Lösung des Zwillingsparadoxon zu glauben.
b) Rückreise: x ist positiv, v in Richtung abnehmende x – dann negativ:
tE = 5J ; xE = 3,0LJ > t´R = [tE – (-v)*xE]*y = (5 + 0,6*3,0)*1,25 = 8,5J !!!
Etwas stimmt hier nicht! Was nicht stimmt, sind die Startkoordinaten des neuen Inertialsystem, in dem die Rakete durch
Umkehrung der Flugrichtung sich jetzt befindet. Diese Startkoordinaten des neuen Inertialsystem bei Erdzeit = 0J
herauszufinden ist etwas umständlich und deswegen können wir neue Startkoordinaten mithilfe des Zielplanets vergeben.
Das bedeutet, die Rakete, bzw. eine zweite Rakete, ĂĽbernimmt vor Ort die Zeit des Zielplanets. Wenn also auf der Erde
die Uhren 5J zeigen, dann zeigen auch die Uhren auf dem Zielplanet 5J, der momentane Ort der Rakete ist auch beim Zielplanet und gleich 3LJ. Diese Startzeit von 5J mĂĽssen wir bei der Berechnungen als t0 immer abziehen und bekommen Startzeiten tE - t0 = tP - t0 = 0J. Das ist aber auch nichts anderes, als wenn wir die RĂĽckreise als eine getrennte Reise
vom Zielplanet zur Erde bei Startzeit tE = tP = 0J betrachten.
Hier darf man nicht vergessen, dass jetzt die Startkoordinaten räumlich um xSTART = 3LJ verschoben sind. Das Resultat xE – xSTART schreiben wir in die Formel als x1
x´R ist dann entsprechend:
tE = 0J ; xE = 3,0LJ > x´R = [x1 – (-v)*tE)*y = [(3-3) + 0,6*0]*1,25 = 0LJ und bleiben während der ganzen Reise
gleich, da die Punktereignisse vor Ort bei der Rakete sind.
Rechnen wir jetzt die RĂĽckreise:
tE = 0J ; xE = 3,0LJ > t´R = [tE – (-v)*x1]*y = [0 + 0,6*(3,0-3,0)]*1,25 = 0,0J
tE = 1J ; xE = 2,4LJ > t´R = [tE – (-v)*x1]*y = [1 + 0,6*(2,4-3,0)]*1,25 = 0,8J
tE = 2J ; xE = 1,8LJ > t´R = [tE – (-v)*x1]*y = [2 + 0,6*(1,8-3,0)]*1,25 = 1,6J
tE = 3J ; xE = 1,2LJ > t´R = [tE – (-v)*x1]*y = [3 + 0,6*(1,2-3,0)]*1,25 = 2,4J
tE = 4J ; xE = 0,6LJ > t´R = [tE – (-v)*x1]*y = [4 + 0,6*(0,6-3,0)]*1,25 = 3,2J
tE = 5J ; xE = 0,0LJ > t´R = [tE – (-v)*x1]*y = [5 + 0,6*(0,0-3,0)]*1,25 = 4,0J
Das Gleiche bekommen wir, wenn wir die Ereignisse bei der Rakete belassen, das Ganze jedoch aus dem Zielplanet beobachten. Wie gehabt, tE = tP und Start bei tE = tP = 0J.
Hinreise: Vom Zielplanet gesehen ist x jetzt negativ, v in Richtung zunehmende x – positiv.
tP = 0J ; xP = 3,0LJ > t´R = [tP – v*(-x1)]*y = [0 + 0,6*(3,0-3,0)]*1,25 = 0,0J
tP = 1J ; xP = 2,4LJ > t´R = [tP – v*(-x1)]*y = [1 + 0,6*(2,4-3,0)]*1,25 = 0,8J
……………………………………………………………………….
tP = 5J ; xP = 0,0LJ > t´R = [tP – v*(-x1)]*y = [5 + 0,6*(0,0-3,0)]*1,25 = 4,0J
Rückreise: x bleibt negativ, v in Richtung abnehmende x – auch negativ.
tP = 0J ; xP = 0,0LJ > t´R = [tP – (-v)*(-xP)]*y = (0 - 0,6*0,0)*1,25 = 0,0J
tP = 1J ; xP = 0,6LJ > t´R = [tP – (-v)*(-xP)]*y = (1 - 0,6*0,6)*1,25 = 0,8J
……………………………………………………………………….
tP = 5J ; xP = 3,0LJ > t´R = [tP – (-v)*(-xP)]*y = (5 - 0,6*3,0)*1,25 = 4,0J
Das wären die „Traumresultaten“ für Relativisten, die die Spezielle Relativitätstheorie aber auch die Lorentztransformation nicht so ganz verstanden haben. Was ist bei dieser Konstellation zu beachten – die Ereignisse fanden auf der Rakete statt, d.h. eine Betrachtung von Lichtlaufzeiten bis und von Ereignisort aus der Sicht der „bewegten“ Raketenbeobachter findet nicht statt. Nach einer Auswirkung der Invarianz der Lichtgeschwindigkeit, aber auch nach einer sinnvollen Anwendung der LT hier zu suchen, ist irrelevant, sogar lächerlich.
2. Wie wäre es, wenn wir die Ereignisse jetzt auf die Erde postieren?
a) Hinreise: x ist positiv, v in Richtung zunehmende x – auch positiv:
xE = 0,0LJ und bleibt, da das Ereignis ständig vor Ort auf der Erde stattfindet.
tE = 0J ; xE = 0,0LJ > t´R = (tE – v*xE)*y = (0 – 0,6*0,0)*1,25 = 0,00J
tE = 1J ; xE = 0,0LJ > t´R = (tE – v*xE)*y = (1 – 0,6*0,0)*1,25 = 1,25J
tE = 2J ; xE = 0,0LJ > t´R = (tE – v*xE)*y = (2 – 0,6*0,0)*1,25 = 2,50J
tE = 3J ; xE = 0,0LJ > t´R = (tE – v*xE)*y = (3 – 0,6*0,0)*1,25 = 3,75J
tE = 4J ; xE = 0,0LJ > t´R = (tE – v*xE)*y = (4 – 0,6*0,0)*1,25 = 5,00J
tE = 5J ; xE = 0,0LJ > t´R = (tE – v*xE)*y = (5 – 0,6*0,0)*1,25 = 6,25J !!!
Um dieses Ergebnis von 6,25J zu verstehen, betrachten wir jetzt auch die räumlichen Koordinaten, da jetzt die Ereignisse nicht mehr auf der Rakete stattfinden:
tE = 0J ; xE = 0,0LJ > x´R = (xE – v*tE)*y = (0,0 – 0,6*0)*1,25 = 0,00LJ
tE = 1J ; xE = 0,0LJ > x´R = (xE – v*tE)*y = (0,0 – 0,6*1)*1,25 = -0,75LJ
tE = 2J ; xE = 0,0LJ > x´R = (xE – v*tE)*y = (0,0 – 0,6*2)*1,25 = -1,50LJ
tE = 3J ; xE = 0,0LJ > x´R = (xE – v*tE)*y = (0,0 – 0,6*3)*1,25 = -2,25LJ
tE = 4J ; xE = 0,0LJ > x´R = (xE – v*tE)*y = (0,0 – 0,6*4)*1,25 = -3,00LJ
tE = 5J ; xE = 0,0LJ > x´R = (xE – v*tE)*y = (0,0 – 0,6*5)*1,25 = -3,75LJ !!!
Welcher Schlauberger wird jetzt behaupten, t´R wäre die Eigenzeit der Rakete und dass die reale Zeit (Uhren) in der Rakete langsamer verlaufen soll? Aus letzten Berechnungen ergibt sich, dass bei Erdzeit = 4J, die Rakete den Zielplanet schon erreicht haben sollte und die Raketenuhren bereits 5J zeigen müssten.
b) Rückreise: x ist positiv, v in Richtung abnehmende x – dann negativ, die räumlichen Startkoordinaten sind
xE – xSTART = 0LJ – 3LJ = -3LJ – das Resultat schreiben wir in die Formel als -x1. Die Startzeitkoordinaten sind auch verschoben, dazu aber später – s. ganz unten – Punkt 4.
tE = 0J ; xE = 0,0LJ > t´R = [tE – (-v)*(-x1)]*y = (0 - 0,6*3)*1,25 = -2,25J !!!
Die negative Zeit bedeutet, dass die Rakete das 0J-Ereignis 2,25J vor dem 0 Zeitabgleich mit der Erde (Zielplanet)
gesehen haben mĂĽsste. Die reale Uhr in der Rakete befindet sich jetzt direkt beim Zielplanet und wurde zugleich vor Ort auf 0J gestellt, d.h. tR = 0J (Eigenzeit)
tE = 1J ; xE = 0,0LJ > t´R = [tE – (-v)*(-x1)]*y = (1 - 0,6*3)*1,25 = -1,00J
tE = 2J ; xE = 0,0LJ > t´R = [tE – (-v)*(-x1)]*y = (2 - 0,6*3)*1,25 = 0,25J
tE = 3J ; xE = 0,0LJ > t´R = [tE – (-v)*(-x1)]*y = (3 - 0,6*3)*1,25 = 1,5J
tE = 4J ; xE = 0,0LJ > t´R = [tE – (-v)*(-x1)]*y = (4 - 0,6*3)*1,25 = 2,75J
tE = 5J ; xE = 0,0LJ > t´R = [tE – (-v)*(-x1)]*y = (5 - 0,6*3)*1,25 = 4,00J
Die räumliche Koordinaten unter Beachtung der verschobenen Startkoordinaten wären:
tE = 0J ; xE = 0,0LJ > x´R = (-x1 – (-v)*tE)*y = (-3,0 + 0,6*0)*1,25 = -3,75LJ !!!
tE = 1J ; xE = 0,0LJ > x´R = (-x1 – (-v)*tE)*y = (-3,0 + 0,6*1)*1,25 = -3,00LJ !!!
tE = 2J ; xE = 0,0LJ > x´R = (-x1 – (-v)*tE)*y = (-3,0 + 0,6*2)*1,25 = -2,25LJ
tE = 3J ; xE = 0,0LJ > x´R = (-x1 – (-v)*tE)*y = (-3,0 + 0,6*3)*1,25 = -1,50LJ
tE = 4J ; xE = 0,0LJ > x´R = (-x1 – (-v)*tE)*y = (-3,0 + 0,6*4)*1,25 = -0,75LJ
tE = 5J ; xE = 0,0LJ > x´R = (-x1 – (-v)*tE)*y = (-3,0 + 0,6*5)*1,25 = 0,00LJ
3. Genauso interessant wird die Situation, wenn die Ereignisse auf dem Zielplanet stattfinden und die „ruhenden“
Beobachter sich auf der Erde befinden. Sonst alles gleich.
Diese Konstellation ist die Standartanwendung der LT – ein Punktereignis, das von den „unbewegten“ und
„bewegten“ Beobachtern entfernt ist. Hier kann man die Auswirkung der Lichtlaufzeiten in Abhängigkeit von der Invarianz der Lichtgeschwindigkeit am besten beobachten, hier ist der Einsatz der LT sinnvoll.
a) Hinreise: x ist positiv, v in Richtung zunehmende x – auch positiv:
tE = 0J ; xE = 3,0LJ > t´R = (tE – v*xE)*y = (0 - 0,6*3,0)*1,25 = -2,25J !!!
tE = 1J ; xE = 3,0LJ > t´R = (tE – v*xE)*y = (1 - 0,6*3,0)*1,25 = -1,00J
tE = 2J ; xE = 3,0LJ > t´R = (tE – v*xE)*y = (2 - 0,6*3,0)*1,25 = 0,25J
tE = 3J ; xE = 3,0LJ > t´R = (tE – v*xE)*y = (3 - 0,6*3,0)*1,25 = 1,50J
tE = 4J ; xE = 3,0LJ > t´R = (tE – v*xE)*y = (4 - 0,6*3,0)*1,25 = 2,75J
tE = 5J ; xE = 3,0LJ > t´R = (tE – v*xE)*y = (5 - 0,6*3,0)*1,25 = 4,00J
Hier kann man auch deutlich sehen, wie t´R von –2,25J bis 4,00J läuft, die Reise bis Zielplanet dauert nach t´R also doch 6,25J. Erneut und deutlich ist auch zu sehen, dass t´R nicht die Eigenzeit der Rakete sein kann. Schon gemerkt? – solange auf der Erde 1J verläuft, verläuft in „bewegten“ IS laut t´R 1,25J !!!
Die räumliche Koordinaten wären:
tE = 0J ; xE = 3,0LJ > x´R = (xE – v*tE)*y = (3,0 – 0,6*0)*1,25 = 3,75LJ !!!
tE = 1J ; xE = 3,0LJ > x´R = (xE – v*tE)*y = (3,0 – 0,6*1)*1,25 = 3,00LJ
tE = 2J ; xE = 3,0LJ > x´R = (xE – v*tE)*y = (3,0 – 0,6*2)*1,25 = 2,25LJ
tE = 3J ; xE = 3,0LJ > x´R = (xE – v*tE)*y = (3,0 – 0,6*3)*1,25 = 1,50LJ
tE = 4J ; xE = 3,0LJ > x´R = (xE – v*tE)*y = (3,0 – 0,6*4)*1,25 = 0,75LJ
tE = 5J ; xE = 3,0LJ > x´R = (xE – v*tE)*y = (3,0 – 0,6*5)*1,25 = 0,00LJ
Schon gemerkt ? – solange aus Erdsicht die Rakete 0,6LJ zurücklegt, fliegt die Rakete laut x´R 0,75LJ, der Zielplanet befindet sich auch nicht auf 3,00LJ, noch weniger auf 2,4LJ, sondern laut x´R auf 3,75LJ.
ĂśberprĂĽfen wir die Ergebnisse:
Der Zielplanet befindet sich laut x´R auf 3,75LJ entfernt, dafür benötigt die Rakete laut t´R 6,25J. Die Reisegeschwindigkeit v ist gleich 0,6c, wie sie auch sein müsste – Invarianz der Geschwindigkeit. Nochmals kann man hier sehen, dass t´R und x´R keine Eigenzeiten und –längen sein können.
b) Rückreise: x ist positiv, v in Richtung abnehmende x – dann negativ, die räumlichen Startkoordinaten sind
xE – xSTART = 3LJ – 3LJ = 0LJ – das Resultat schreiben wir in die Formel als x1
tE = 0J ; xE = 3,0LJ > t´R = [tE – (-v)*x1]*y = (0 + 0,6*0)*1,25 = 0,00J
tE = 1J ; xE = 3,0LJ > t´R = [tE – (-v)*x1]*y = (1 + 0,6*0)*1,25 = 1,25J
tE = 2J ; xE = 3,0LJ > t´R = [tE – (-v)*x1]*y = (2 + 0,6*0)*1,25 = 2,50J
tE = 3J ; xE = 3,0LJ > t´R = [tE – (-v)*x1]*y = (3 + 0,6*0)*1,25 = 3,75J
tE = 4J ; xE = 3,0LJ > t´R = [tE – (-v)*x1]*y = (4 + 0,6*0)*1,25 = 5,00J
tE = 5J ; xE = 3,0LJ > t´R = [tE – (-v)*x1]*y = (5 + 0,6*0)*1,25 = 6,25J !!!
Die räumliche Koordinaten unter Beachtung der verschobenen Startkoordinaten wären:
tE = 0J ; xE = 3,0LJ > x´R = (x1 – (-v)*tE)*y = (0,0 + 0,6*0)*1,25 = 0,00LJ
tE = 1J ; xE = 3,0LJ > x´R = (x1 – (-v)*tE)*y = (0,0 + 0,6*1)*1,25 = 0,75LJ
tE = 2J ; xE = 3,0LJ > x´R = (x1 – (-v)*tE)*y = (0,0 + 0,6*2)*1,25 = 1,50LJ
tE = 3J ; xE = 3,0LJ > x´R = (x1 – (-v)*tE)*y = (0,0 + 0,6*3)*1,25 = 2,25LJ
tE = 4J ; xE = 3,0LJ > x´R = (x1 – (-v)*tE)*y = (0,0 + 0,6*4)*1,25 = 3,00LJ
tE = 5J ; xE = 3,0LJ > x´R = (x1 – (-v)*tE)*y = (0,0 + 0,6*5)*1,25 = 3,75LJ !!!
Auch aus dieser Konstellation ergibt sich für Leute, die glauben, dass t´ und x´ Eigenzeiten und Eigenlängen seien und daraus das Zwillingsparadoxon zu rechtfertigen versuchen, dass während auf der Erde 10 Jahre vergangen sind, sind in der Rakete 12,5 Jahre vergangen, was genauso falsch wäre, wie die Behauptung, dass solange auf der Erde 10 Jahre vergangen sind, sind es in der Rakete nur 8 Jahre.
Aus 2. und 3. ist ersichtlich, dass t´R nicht die Eigenzeit der Rakete sein kann. t´R zeigt -2,25J in dem Moment, als die
Rakete gerade vor Ort bei der Erde ihre Uhren auf 0 gestellt hat, d.h. zu diesem Zeitpunkt zeigten die realen Raketenuhren direkt vor Ort 0J – und das ist die Eigenzeit der Rakete.
Die Berechnungen zeigen auch überdeutlich, dass die Weltlinie des Zielplanets nach Meinung der „unbewegten“ Beobachter für die „bewegten“ sich wo anders befinden müsste.
Für Schlauberger, die die Differenz von 2,25 Jahren durch die Relativität der Gleichzeitigkeit (RdG) verschwinden sehen
möchten: Natürlich handelt es sich bei der Verschiebung von 2,25J um die RdG. Die RdG existiert aber nicht als
eigenständigen Effekt in der SRT. Sie ist nur eine Folge aus der ZD und LK und stellt keine metaphysischen Zeitsprünge
dar. Uhren können nicht plötzlich, mir nichts dir nichts, Zeitsprünge machen, nur weil irgendein entfernter Beobachter
sich nach der Uhrzeit erkundigt. Die gleiche RdG wäre auch für die fragwürdigen Resultaten in Punkt 1 verantwortlich.
4. Die richtigen Startkoordinaten in allen Fällen, wo entweder das Ereignis oder die „bewegten“ Beobachter entfernt sind,
d.h. sie haben keine gemeinsamen bei 0 Startkoordinaten, reicht nicht, wenn nur die räumliche Verschiebung berücksichtigt wird – im unseren Beispiel x = 3LJ und daraus x´ = 3,75LJ – sondern muss dazu berücksichtigt werden, dass auch die zeitlichen Startkoordinaten mit t´ = 1,25J verschoben sind. Das ist genau die Zeit, die die Rakete benötigt,
um diese „erweiterte“ um 0,75LJ Strecke zu durchfliegen. Wird auch diese Korrektur vorgenommen, bekommen wir die vorgeschriebene Symmetrie (Relativitätsprinzip) – s. auch die Minkowski-Diagramme – dann werden überall t´ und x´ im
Beispiel beim Start entsprechend um (-)1,25J und (-)0,75LJ versetzt, demzufolge wird das Ziel bei 5J und 3LJ, bzw.0LJ mit den gleichlautenden Koordinaten aus der Sicht der „unbewegten“ Beobachter zusammenfallen.
Nur mit der Operation xE – xSTART = x1 bekommen wir lediglich die identische Situation, als wenn die Rakete sich in
negativer Richtung von der Erde entfernt und als ob die Startkoordinaten bei 0 zusammenfielen.
--------------------------------------------------------------------------------------------------------------------
Fast alle hier angegebenen Koordinaten kann jeder mithilfe dieses Java-Applets ĂĽberprĂĽfen:
http://www.mathe-online.at/mathint/struct/applet_b_lorentz.html (Zweimal auf den Button klicken!)
Stammt von Relativisten (Embacher u.a.). Leider kann man dort mit verschobenen Startkoordinaten nichts anstellen,
aber auch so mĂĽsste ausreichend Aufschluss gegeben sein.
Auch eine Überprüfung nach t² - x² = t´² - x´², solange man mit den versetzten Startkoordinaten umgehen kann, wird
die Richtigkeit der Berechnungen bestätigen.
Natürlich können wir jetzt auch die Rakete als „unbewegt“, Erde und Zielplanet als die „bewegten“ betrachten. Dann sehen die Gleichungen bei c = 1 und v in c-Einheit so aus:
t´E = (tR – v*xR)*y und t´P = (tR – v*xR)*y
x´E = (xR – v*tR)*y und x´P = (xR – v*tR)*y
Die Resultaten werden aber genauso ernüchternd auf enthusiastische Relativisten wirken, die an Märchen von junggebliebenen Astronauten, zeitdilatierten Myonen und langlebigen Organismen im Schachtel glauben.
------------------------------------------------------------------------------------------------------------
5. Berechnen wir auch den Fall mit den „langlebigen“ Myonen. Sie sollen in einer Höhe von ca. 20km über Erdboden
entstehen und mit fast Lichtgeschwindigkeit in Richtung Erdoberfläche sausen. Nehmen wir eine Geschwindigkeit der Myonen von 0,995c – so bekommen wir einen leicht zu handhabenden y-Faktor von 10.
Postieren wir dort oben einen ruhenden rel. z. Erdoberfläche Beobachter B, und wollen wissen, ob ein Myon die
Erdoberfläche erreichen kann, bzw. wie aus seiner Sicht die Zeiten und Längen aussehen. Das Myon entsteht vor Ort neben dem Beobachter und beide Uhren starten bei 0ms. Das Ereignis ist bei 0ms und auf der Erdoberfläche. Die
Koordinaten des Ereignisses aus Sicht des ruhenden Beobachters wären tB = 0ms und xB = 20km = 0,0667Lms
t´M = (tB – v*xB)*y = (0 - 0,995*0,0667)*10 = ca. -0,666ms !!!
x´M = (xB – v*tB)*y = (20 – 0,995*0)*10 = 200km !!!
Was bedeuten diese Zahlen, bzw. Koordinaten der Erdoberfläche (Ereignis)? Das Myon befand sich doch beim Entstehung tB = 0ms neben dem Beobachter? – Dass z. Zeitpunkt 0ms, der zugleich der Entstehung des Myons entspricht, müsste das Myon nach Meinung des ruhenden Beobachters die Erdoberfläche 200km entfernt sehen, das aber
vor 0,666ms. Es verbleiben ihm noch 2km zur Erdoberfläche, nachdem es schon 198km geflogen ist, und nachdem bei ihm schon 0,666ms vergangen sind. Und das bedeutet, dass das Myon längst zerfallen ist, wenn t´M seine Eigenzeit wäre.
Genau die gleichen Ergebnisse bekommen wir, wenn der „ruhende“ Beobachter sich auf der Erde befindet und das Ereignis die Entstehung des Myon wäre, aus Sicht des Myons aber das Ereignis auf der Erdoberfläche – gegenseitiges Beobachten.
Versetzen wir uns ins Inertialsystem des Myons, das jetzt „ruhend“ ist, dann sind aus seiner Sicht die Koordinaten des Ereignisses auf der Erdoberfläche tM = 0ms und xM = 20km und das sind die Eigenzeit und Eigenlänge des Myons. Es kommt ihm kein Ereignis mit v = 0,995c entgegen, da ein Ereignis immer unbewegt ist. Wer jetzt der „bewegte“ ist, ist der Beobachter, der mit –v (-0,995c) vom Entstehungsort sich in negative Richtung entfernt. Und wenn das Myon sich für die vom Beobachter zu sehenden Koordinaten der Erdoberfläche bei tM nicht interessiert, dann wird die Reise des Myons bis Erdoberfläche, oder auch anders ausgedrückt – die Reise des Ereignisortes (Erdoberfläche, Ort der Ereignisabfolge) bis Myon, klassisch berechnet und ist nichts anderes als tM = 20km/0,995c.
Oder nochmals bei Zeitpunkt 0ms = Zeitpunkt der Entstehung des Myons und voraussichtliche Reisezeit bis zur Erdoberfläche:
a) Die Daten im Myon-IS nach Meinung des ruhenden Beobachters:
t´M_0 = -0,666ms
x´M_0 = 200km
Delta t´M = t´M_Erde – t´M_0 = 2km/0,995c – (-0,666ms) = 0,0067ms + 0,666ms =
0,67ms
b) Die realen Daten vor Ort im Myon-IS:
tM_0 = 0ms
xM_0 = 20km
Delta tM = tM_Erde – tM_0 = 20km/0,995c - 0 =
0,067ms
Die mittlere Zerfallsrate der Myonen beträgt 0,0022ms. Dass diese mittlere Lebensdauer der Myonen in bremsenden Feststoffen gemessen wird, wo nicht mal bekannt ist, wie „alt“ die Myonen bereits beim Eintreffen sind, brauche nicht zu kommentieren.
Für Leute, die mit der SRT und LT umgehen können, ist klar was t´ und x´ bedeuten und dass ein Zwillingsparadoxon in
der SRT nichts zu suchen hat.
Wie ist es möglich, von Invarianz der Eigenzeit und Eigenlänge zu sprechen und zugleich reale Zeitdilatation und Längenkontraktion befürworten?
© Ljudmil Daskalow
Erstfassung: 10.01.2010
Letzte Aktualisierung: 19.01.2010
Zitate und sinngemäße Wiederdarstellungen dürfen nur mit Quellenangabe veröffentlicht werden!