Zwillingsparadoxon

Die vorgesehene Erläuterung der Begriffe Uhr, Uhrzeit, Zeit ist leider noch nicht fertig, dafür aber ist hier das „Zwillingsparadoxon“ in neuem Licht vorgestellt.

Das Zwillingsparadoxon (ZP) in einem Minkowski Diagramm (MD).
Eingehende Untersuchung im Rahmen der Relativitätstheorie und die Folgen daraus.

Ein für alle Mal möchte ich das Geschwätz über das „geklärte“ Zwillingsparadoxon mittels „Systemwechsel“ in einem Minkowski-Diagramm entkräften und einigen Relativisten vorführen, dass sie erhebliche Lücken in Elementarphysik aufweisen.

Zuerst beschreibe ich für uneingeweihte Leser das Zwillingsparadoxon:
Nach einer Behauptung von Einstein, sollen „bewegte“ Uhren nachgehen. Diese Behauptung ist jedoch physikalisch nicht haltbar und widerspricht zugleich den Grundpostulaten der Speziellen Relativitätstheorie (SRT). Nach der SRT, und genauer dem Relativitätsprinzip, müsste jeder Beobachter in einem Inertialsystem behaupten, er sei der Unbewegte und der andere wäre der Bewegte. Dieses Grundpostulat der SRT findet sich auch in der mathematischen (die Lorentztransformation - LT) und grafischen (Minkowskidiagramm - MD) Bekleidung wieder.
Dieser Widerspruch wurde zuerst von Langevin 1911 angesprochen. In Folge versuchte Einstein und seine Anhänger dieses Paradox irgendwie aufzuklären und zu einem scheinbaren Widerspruch (Paradoxon) herunterspielen.
So entstand das berühmt berüchtigte Zwillingsparadoxon und lautet: Einer von zwei Zwillingen fliegt mit einer Rakete und mit großer Geschwindigkeit zu einem weit entfernten Planet und zurück. Für ihn, den Reisenden, vergehen bis Rückkehr auf die Erde z.B. 8 Jahre. Laut Einsteins Behauptung würde er seinen auf der Erde gebliebenen Zwillingsbrüder (der Erdling), jedoch viel älter vorfinden.
Die Begründung lautet: Die Zeit ist für den Reisenden langsamer verlaufen, da er schnell und weit gereist ist und in den Augen des Erdlings der Bewegte wäre.
Jetzt kommt aber das Gegenargument als Folge des Relativitätsprinzips, dass der Reisende genauso behaupten kann, er sei in Ruhe gewesen und sehen konnte, wie die Erde sich von ihm entfernte und später näherte und folglich sei der Erdling der Bewegte und müsste jünger sein.

Einstein und Anhänger befanden sich in der Zwickmülle und versuchten das Problem mit den Beschleunigungen, die naturgemäß beim Reisenden während Start, Wende und Landung auftreten, die aber nicht im Rahmen der SRT lagen, wo diese Zeitdilatation ausschließlich durch den inertialen Flug begründet war, zu lösen. Prompt kam auch das Gegenargument - man könnte die Reisedauer wesentlich verlängern, so dass die Beschleunigungsphasen kaum ins Gewicht fielen. Dazu habe ich noch ein vernichtendes Gegenargument, weiter unten, aufgestellt, nach dem sich sogar herausstellt, dass eigentlich der Erdling der jüngere bei der Ankunft sein müsste. Einsteins Versuch 1918 das ZP im Rahmen der Allgemeinen Relativitätstheorie (ART) in einer fiktiven Diskussion mit einem „Kritikus“ zu lösen, kann man nur als einen schlechten Witz betrachten, in dem er sich bis zu den Knochen blamiert. Dort spricht er selbst die kurzen Beschleunigungsphasen an, die angebliche Zeitdilatation während des langen Inertialfluges behandelt er aber auch als nicht existent. Eine späte Einsicht, aber immerhin, irren ist menschlich, die SRT ist vorläufig gerettet. Es bleiben also nur die Beschleunigungen als Ursache? Weiter unten - Abschnitt VIII, wo die Zeitdilatation während Beschleunigungen angesprochen ist, halte ich eine Überraschung für dich, lieber Albert, parat.

Wann und von wem - ich weiß es nicht (v. Laue?) - tauchte in der Physikwelt eine neue „Lösung“ des Paradoxes. Die Reisekonstellation wurde in einem Minkowski-Diagramm behandelt, und man berief sich auf einen angeblichen Inertialsystemwechsel, bei dem ein Zeitsprung auftreten sollte. Und so lebten die Märchen von einem junggebliebenen reisenden Zwilling in allen „physikalischen“ Publikationen bis heute.

Jetzt ist die Zeit, um paar Worte über das Minkowski-Diagramm (MD) zu sagen: Dieses Diagramm ist eng mit der Minkowskis Theorie (Weltpostulat) verbunden. Sie wiedergibt graphisch und anschaulich die Lorentztransformation (LT) und die Grundaussagen der SRT.
Bei Minkowski ist die s.g. Zeitdilatation nur scheinbar, d.h. die Uhren von zueinander bewegten Beobachter laufen zu jeder Zeit synchron, nur jeder Beobachter SIEHT die Uhr des anderen nachgehen. Dieser Effekt ist symmetrisch und entspricht vollkommen der SRT und LT, widerspricht jedoch der Einsteinsbehauptung vom einseitigen und geisterhaften realen Nachgehen einer der Uhren. Um die Äthervorstellung mit dem Michelsons Experiment zu versöhnen, erfand Minkowski den „krummen“ Raum, und das war bei ihm real, nicht verstellte Uhren, wie bei Einstein.
In Folge dessen, müsste die Darstellung des ZP in einem MD jedem eingeweihten Physiker höchst abenteuerlich erscheinen. Und wie wir sehen werden, ist diese „Lösung“ des Zwillingsparadoxons in einem MD offensichtlich nur Spaß eines Witzboldes, oder der Erfinder, wie auch Nachahmer, nicht die geringste Ahnung von Relativitätstheorie, Lorentztransformation und Minkowski-Diagramm hatte, bzw. haben.

Betrachten wir zuerst ein übliches Minkowski-Diagramm und klären einige Grundzüge - dafür ist die Zeichnung MD vorgesehen.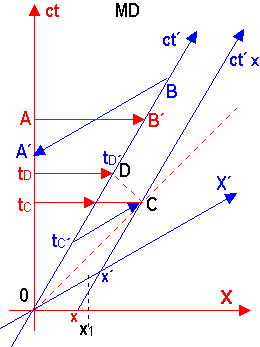

1. Bei Minkowski laufen alle Uhren synchron, die Lichtgeschwindigkeit ist in beiden Inertialsystemen konstant und gleich, obwohl sie relativ zueinander bewegt sind. Richtiger nach der SRT ist: Die Lichtgeschwindigkeit wird in allen Inertialsystemen gleich c gemessen . Dass die Zeitangaben im “bewegten” Inertialsystem (ct´-Achse) gedehnt erscheinen, hat mit zeitdilatierten Uhren nichts zu tun - das ist nur eine graphische Folge aus der Neigung der Raumachse und scheinbaren Dehnung der Längen und Maßstäbe, wie wir später sehen werden.
In rot ist alles was der „unbewegte“ - und in blau alles was der „bewegte“ Beobachter SIEHT. Unter “SEHEN” ist immer Messen mit Licht- oder Funksignalen in Zweiwegverfahren gemeint und entspricht der Einsteins Synchronisationsvorschrift (Poincaré-Synchronisation), auch Synchronisationsmethode genannt.
2. Zeitvergleich zwischen zwei zueinander bewegten Inertialsystemen (IS). Der Unbewegte in Zeitpunkt A sieht im bewegten IS nicht B, sondern B´, oder tA = tB/y (y verwende ich hier als Symbol für Gamma = 1/sqrt(1-v²/c²) ) und umgekehrt, der Bewegte sieht in Zeitpunkt B nicht A, sondern A´, oder tB = tA/y. Die LT ist bewahrt. Jeder Beobachter sieht die Zeit des anderen mittels eine Verbindungslinie, die parallel zu seiner Raumachse X bzw. X´ verläuft.
3. Sehen wir jetzt das Gedankenexperiment von §2 der „Zur Elektrodynamik bewegter Körper“ in diesem MD. Ein Stab (bewegtes IS) dessen Enden die zwei Weltlinien ct´ und ct´x bilden, und es wird ein Lichtsignal (rot punktiert) von 0 nach C geschickt, dort reflektiert es und gelangt zurück zum D.
a) Längenkontraktion (LK) - hier bei Minkowski ist alles klar angegeben. Die Ruhlänge L = 0 bis x1; die Längen und Maßstäbe SIND im bewegten IS *y gedehnt, oder 0 bis x´ = L*y; die Unbewegten SEHEN eine verkürzte Länge 0 bis x = L/y, wie auch umgekehrt. Diese Dehnung der bewegten Länge in einem MD ist genauso nicht real, sondern nur eine Folge der graphischen Darstellung, bzw. der Drehung der Koordinatenachsen und bedeutet, dass x1 und x´ den gleichen Wert auf der entsprechenden Achse haben.
b) Die Zeiten: Die Unbewegten messen 0 bis C = x/(c-v) = tC und C bis D = x/(c+v) = tD-tC.
Die Bewegten messen 0 bis C = x´/c und C bis D = x´/c, oder tC´ = ½ tD´. Sie messen Vorgänge zwischen unbewegten Punkten in ihrem System und ist klar, dass die Ableselinie parallel zur JETZT-Achse X´ (Raumachse, Gleichzeitigkeit) verläuft.

I. Um oft missverstandene Betrachtungen und Deutungen in einem MD ins rechte Licht zu rücken, betrachten wir als nächstes ein völlig symmetrisches Raum-Zeit-Diagramm (MD) S - unten in der Mitte.
Die Angaben: Zwei Zwillinge reisen gleichzeitig mit identischen Raumschiffen und Absichten von der Erde in entgegengesetzte Richtungen ab. Sie fliegen mit gleicher Geschwindigkeit bis gleich entfernen Zielplaneten, kehren dort um, und fliegen wieder völlig symmetrisch zurück zur Erde. Die Weltlinie der Erde ist die vertikale schwarze in der Mitte. Die Inertialgeschwindigkeit beträgt 0,333c rel. z. Erde, oder nach der relativistischen Geschwindigkeitsaddition 0,6c rel. zueinander. Die Zielplaneten (unbewegt rel. z. Erde) auf Abstand von je 1,66LJ. Am Zielplanet gelandet, werden die Uhren zwischen beiden Zwillingen erneuert auf 0 gestellt (real und nach SRT - kein Problem - beide sind zu diesem Zeitpunkt unbewegt zueinander) - das habe ich absichtlich eingeführt, um einige Sachverhalte verständlicher zu machen. Die Zwillinge benennen wir Rot (links, alles in rot betrifft seine Sicht) und Blau (rechts, alles in blau betrifft seine Sicht). ct-h - die Zeitachse beim Hinflug; ct-r - beim Rückflug; X-h - die Raumachse beim Hinflug; X-r - beim Rückflug.

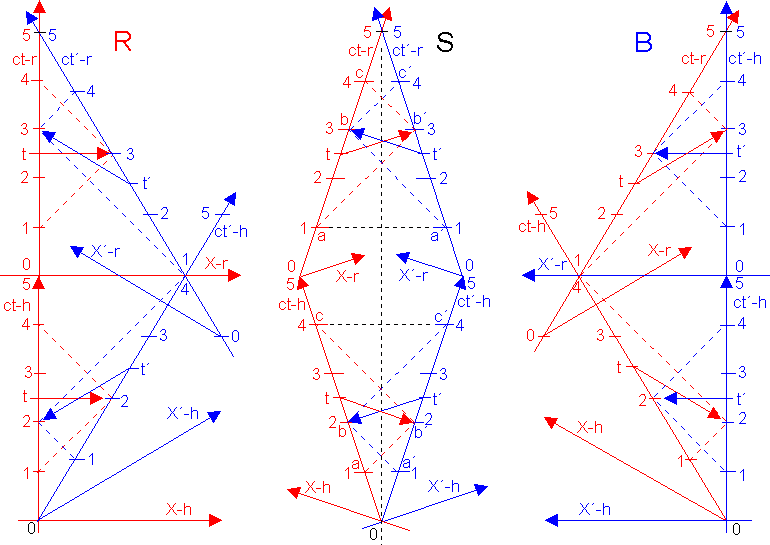
So, wir wollen jetzt nicht nur die scheinbare Zeitdilatation zwischen den Zwillingen betrachten, sondern sie auch physikalisch begründen , was meistens in den Lehrbüchern fehlt (warum wohl?). Dass bei so einer symmetrischen Situation, die Uhren der Zwillinge synchron laufen und sie auch nur symmetrischen Zeitdilatation beobachten werden, ist unbestritten, egal nach welcher auch Theorie. Nach einem Jahr Reisezeit, wollen die Zwillingen sich erkundigen, was mit der Zeit (Uhranzeigen) des anderen, aus ihrer Sicht, geschieht.

Wie ist es möglich Zeitanzeigen mittels Licht- oder Funksignale zu vergleichen? Es würde wenig nützen, wenn einer einen Funkspruch mit seiner Zeitangabe sendet - der andere wüsste nicht, wo sich der erste befindet und wie lange das Signal unterwegs war. Die einzige Möglichkeit besteht darin, dass der eine ein Signal zum anderen sendet, dort reflektiert und mit einem Zeitstempel versehen, zurück empfangen wird (Einsteins Synchronisationsvorschrift). Jetzt muss man was außerordentlich wichtiges beachten: Nach der SRT bewegt sich das Signal mit c relativ zu jedem Inertialsystem (Invarianz der Lichtgeschwindigkeit), und das ist die Grundlage der s.g. Relativität der Gleichzeitigkeit (RdG). Das bedeutet auch, jeder Zwilling braucht sich keine Gedanken darüber machen, dass der andere (Ziel) während der Messung ihm gegenüber bewegt ist.

Rot schickt zum Zeitpunkt a ein (Licht-) Funksignal zum Zwilling Blau, dort - b´- wird sofort mit Zeitstempel geantwortet (reflektiert) und er empfängt das Signal zum Zeitpunkt c. Rot mach jetzt die Rechnung: Ich habe das Signal um 1,00J (a) geschickt, zurück ist es um 4,00J (c) angekommen. Das Signal braucht also bis hin und zurück 3J, oder dort muss es bei
½ 3J + 1J = 2,5J meiner Zeit gewesen sein. Jetzt schaut er sich den Zeitstempel an und wundert sich nicht - es steht 2J. Aha, sagt er, alles nach SRT und LT stimmt - die rel. Geschwindigkeit zwischen uns ist 0,6c, dann ist Gamma (y) = 1,25;
t´ = t/y = 2,5/1,25 = 2J . Blau unternimmt den gleichen Experiment - bei a´ senden, bei b wird reflektiert und bei c´ wieder empfangen - seine Daten und Berechnungen sind identisch, wie vom Rot - ja, sagt auch er, alles nach SRT und LT stimmt. Wir betrachten das MD und können auch bestätigen - ja, auch dort stimmt alles. Diese Art Messungen mit Lichtstrahlen ist nichts andere, als die praktische Anwendung der Lorentz Transformation - d.h. statt Messung können wir jederzeit die LT anwenden und erfahren, was ein Beobachter zu bestimmtem Zeitpunkt in einem fremden Inertialsystem (IS) MESSEN würde.

Nun, nachdem die Zwillinge ihre Ziele erreicht haben, stellen sie ihre Uhren wieder auf 0 und treten die Rückreise an. Nach einem Jahr vergleichen sie die Zeiten, wie gehabt, erneuert. Da sie nicht so gut mit der SRT, LT und MD vertraut sind, werden die Ergebnisse sie überraschen. Jetzt sieht jeder die Zeit des anderen VORGERÜCKT. Rot berechnet den Zeitpunkt der Reflektion mit 2,5J - wie beim Hinfahrt, der Zeitstempel lautet aber 3J (2J beim Hinfahrt). Die gleichen Beobachtungen macht auch Blau. Sie messen nochmals und stellen fest, dass die Zeit des anderen weiterhin vorgerückt erscheint, aber die Zeitspanne zwischen beiden Messungen ein Nachgehen der anderen Uhr anzeigt. Interessanterweise müssen sie jetzt die Uhrzeiten nach
t´= t_n- (t_n - t)/y, wobei t_n die Ankunftszeit auf der Erde ist, und nicht nach t´= t/y, wie beim Hinflug, berechnen; die Zeitinterwalen aber doch nach t´= t/y, was die scheinbar vorgerückte Zeit stetig aufholt.
Auf der Erde angekommen, suchen sie RT-Gelehrten auf, um nach ihren ungewöhnlichen Resultaten zu befragen. Die Gelehrten meinen, seid beruhigt, so muss es auch nach richtiger Anwendung der SRT und LT sein - beim Hinflug habt ihr euch voneinander entfernt, d.h. die Bewegung erfolgte in wachsende X-Richtung und ausgehend von einem identischen Ort, beim Rückflug jedoch, habt ihr euch zueinander bewegt, d.h in schrumpfende X-Richtung und ausgehend von zwei nichtidentischen Orten. Da die Zeit- und Raumachsen beim Anfang des Rückfluges verschoben sind (RdG), muss man der Einfachheit halber die Ankunftszeit, dort wo die Zeitachsen zusammenfallen, als Basis nehmen und rückrechnen. Auch bei richtiger Anwendung der LT unter Berücksichtigung der Startorte bekommt ihr den gleichen Resultat, dort darf man aber nicht vergessen das Vorzeichen der Geschwindigkeit zu wechseln und von t´ die Differenz aus der Verschiebung der Gleichzeitigkeitsachsen abzuziehen.
Wir betrachten das MD und können auch bestätigen - ja so muss es sein und alles stimmt. Würden wir die Zeiten in dieser Rückflugphase umgekehrt berechnen, d.h. von Ankunft zurück zum Start, was wiederum ein Entfernen voneinander bedeutet (wachsender x) - dann passt die Formel t´= t/y, wie beim Hinflug.

Wie kommt diese „Zeitdilatation“ zur Stande, obwohl, wie wir gesehen haben, beide Uhren zu jeder Zeit synchron laufen (s. die schwarzen waagrechten Linien bei 4 und 1(6))? Sie versteckt sich in der postulierten Annahme, dass das Signal (Licht, Funk) zu jedem IS mit gleicher Geschwindigkeit sich ausbreitet (Invarianz der LG) . Ob diese Annahme gerechtfertigt ist, werden wir hier nicht diskutieren und als vorgegeben akzeptieren.

Zeichnen wir jetzt auch je ein MD aus der Sicht des einzelnen Zwillings, der sich in Inertialflug berechtigt als der Ruhende ansieht, bei gleichen Angaben. Seine Koordinaten empfindet er als rechtwinklig zueinander und die Koordinaten des anderen, der er als den Bewegten betrachtet, als die geneigten. Aus der Sicht des Zwillings Rot ist das MD links (R) und aus der Sicht des Zwillings Blau, das rechte MD (B). Obwohl sich absolut nichts geändert hat, nur zeichnerisch anders gestaltet, erscheinen die Sichten ungewohnt. Die Zeitachsen des jeweils „Bewegten“ sind gedehnt und gehen über den früheren Wendepunkt hinaus. Überprüfen wir alles mit den Synchronisationssignalen, nach SRT und LT - alles stimmt, die drei MD sind identisch. In allen drei laufen die Uhren synchron und zeigen vor Ort die gleiche Zeit.
Würde jedoch ein Amateur solches MD sehen, könnte er leicht die ct-Achsen mit realen Zeit- & Ortskalen verwechseln und beschließen, die Zeit des jeweils „Bewegten“ tatsächlich langsamer verläuft, und dass die Umkehr bei 4J stattfindet. Aha, so was „zeigt“ das ZP, würde er meinen. Weit gefehlt, wie aus allen drei Diagrammen mehr als deutlich zu sehen ist. Warum sind die ct-Achsen aber doch auseinander gekommen? Weil das nur eine zeichnerische Darstellung der SRT & LT ist, weil es sich um zwei angekoppelte MD handelt, weil bei Ende der Hinreise und Beginn der Rückreise die Gleichzeitigkeit-Achsen nicht zusammenfallen, und weil die realen Bedingungen, d.h. die Beschleunigungsphasen bislang unterschlagen wurden, was wir später nachholen werden.
Es findet hier kein Zeit- oder Raumsprung statt, es handelt sich nur um eine graphisch bedingte Verschiebung der Koordinatenursprung durch die Drehung der Raumachse. Die außerhalb vom „Wendepunkt“ verlaufenden ct-Achsen dürfen auf keinem Fall vergessen werden, ansonsten hat man von der Relativität der Gleichzeitigkeit & Invarianz der Lichtgeschwindigkeit nichts verstanden. Was dieses Herausragen der ct´-Achsen in einem MD bedeutet, werden wir später bei der Längenkontraktion erfahren.

Was haben wir bis hierher gelernt? Dass die realen Uhranzeigen und Uhrgang, unmittelbar am Ort betrachtet (Hier-Achse - ct), synchron laufen - Invarianz der Eigenzeit. Beim Vergleich mittels Funk-, Lichtsignalen ERSCHEINT die fremde, relativ bewegte Uhr anders zu laufen. Dieser Effekt geschieht symmetrisch, was nochmals die Synchronität der Uhren bestätigt, und wird in der SRT als Zeitdilatation bezeichnet. Es handelt sich also nicht um tatsächlich dilatierte Uhren, sondern nur um einen SCHEINeffekt , der Einstein in seiner Voreiligkeit mit einem SEINeffekt verwechselte.

Ein Koordinatensystemwechsel erfolgt auch zu keiner Zeit. Im Falle des ZP existiert ein einziges sinnvolles Koordinatensystem - die X-Achsen sind zu jeder Zeit die Verbindungslinie zwischen Erde und Zielplanet. Was sich hier ändert, sind nur die Wahrnehmungslinien (RdG), die sich analog zu der relativen Geschwindigkeit und Richtung, und das nur zeichnerisch, in einem MD allmählich neigen.

II. Widmen wir uns jetzt dem überall anzutreffenden „Minkowski-Diagramm“, das angeblich das Zwillingsparadoxon „begründet“ und versuchen die einzelnen Phasen nach der SRT und LT zu überprüfen. Der SRT-Amateur, oder Spaßvogel, der diese Erfindung in die Welt gesetzt hat, konnte offensichtlich nicht rechnen. Ich habe zu dem bekannten MD nur die Sichtlinien des Erdlings hinzugefügt und, um einen Vergleich zu haben, zusätzlich Jahreszahlen, beginnend von 0 bei der Umkehr angegeben. Das ist legitim, da gerade bei der Wende befinden sich beide Zwillinge in Ruhe zueinander, bzw. man kann jederzeit so eine, nur Rückkehr-Situation, mit gleich gestarteten Uhren reproduzieren.

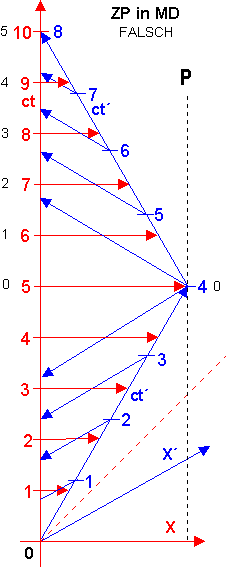Wie wir sehen, ist dort ein Zeitsprung von 3,2J auf 6,8J aus Sicht des Bewegten. Etwas kann hier nicht stimmen, Zeitsprünge gibt es nur in einer Metaphysik und würde bedeuten, dass der Reisende während der Wende gleichzeitig alle Zeiten zwischen 3,2J und 6,8J sieht - ob er nicht zu schielen beginnt? Nach welcher Formel oder Aussage aus der SRT, LT oder Weltpostulat wurde diese Situation berechnet? Vergleichen wir dieses Diagramm mit dem MD - oben links, aus der Sicht des roten Zwillings und wo die Uhren synchron zueinander liefen. Na, so was? Bis zur Wende sind sie identisch, und das beweist, dass auch in diesem falschen Diagramm die Uhren synchron laufen müssen. Würde die „reisende“ Uhr tatsächlich langsamer laufen, dann müsste man mit doppelter Gamma berechnen, folglich würden aber die Invarianz der LG, LT und MD nicht mehr stimmen.

Gehen wir ins Detail und fragen, was sieht der Erdling in Punkt 5,00J seiner Zeit? Das ist genau der Moment, als beide zueinander unbewegt, bzw. mit extrem niedriger rel. Geschwindigkeit sich befinden. Gamma ist 1. Der Erdling müsste also 5J beim Reisenden sehen. In diesem Diagramm steht aber 4. Nun, überprüfen wir die Lage, als der Reisende sich 1min vor und 1min nach der Wende befand. So, eine Minute vor - sieht er 3,2J und eine Minute nach - 6,8J beim Erdling stehen. Oder, während bei ihm 2min vergangen sind, sind es beim Erdling 3,6 Jahren, obwohl, wie schon oben aufgeführt, sich beide zu diesem Zeitpunkt kaum in relativer Bewegung befanden. Nach welcher Formel und Gamma wurde das berechnet? Wie wurde das gemessen? Offensichtlich sind viele Physiker einem Spaßvogel auf dem Leim gegangen und die ct-Achsen eigenwillig beschnitten - s. oben die Diagrammen R und B.

Betrachten wir jetzt die Situation so, als wenn der Reisende sich längere Zeit auf dem Zielplanet aufhielt (rel. Geschwindigkeit = 0) und genügend Gelegenheit hatte, seine Uhr mit der irdischen zu synchronisieren. Bei 0 Uhr (schwarze Jahreszahlen) startet er zurück zur Erde. Er beschleunigt „kurz“ und fliegt mit Inertialgeschwindigkeit von 0,6c. Bereits nach der extrem kurzen Beschleunigungsphase, sagen wir 1 Stunde, sieht er auf der Erde 1,8J - wieder die Frage, nach welcher Formel und Gamma kann man das berechnen?
Was sieht der Erdling, nachdem bei ihm 1 Jahr vergangen ist - aha, 0,8J beim Reisenden, stimmt, wenn Gamma 1,25 ist und aber nach der falschen Formel gerechnet wurde (s. oben - rechnen bei schrumpfendem x). Jetzt berechnen wir nach der gleichen Formel, was der Reisende nach 1J (blau 5) sieht. Gamma ist gleich und er müsste auch 0,8J beim Erdling sehen. Symmetrie und Relativitätsprinzip müssen eingehalten werden, so sagt die SRT, LT und MD. Was sehen wir auf der Zeichnung? Der Reisende sieht 2,6J statt 0,8J!!!
Und wie wäre es, wenn wir in diesem Diagramm die Einsteins Synchronisationsvorschrift anwenden, und wie oben mit Lichtstrahlen die Angaben überprüfen? Wie wäre es, wenn der Ereignisort sich auf der Erde befindet? - s. dazu Anlage unter Punkt V

Müssen wir uns länger mit dieser Parodie eines Minkowski-Diagramms beschäftigen?

III. Kommen wir jetzt zum ZP in einem richtigen und nachprüfbaren MD. Wie wir gesehen haben, passieren einige Verschiebungen der gegenseitig beobachteten Zeit gerade während Start, Wende und Ankunft, und deswegen nehmen wir genau diese Phasen unter der Lupe. Es werden also nicht Beschleunigungskräfte, die auf die Uhren irgendeine Wirkung ausüben, sondern nur die zeitliche Änderung der Geschwindigkeit und ihre Auswirkung auf die beobachteten Uhrzeitangaben untersucht.

Was habe ich hier gezeichnet: Der Reisende (bewegter Beobachter) startet von der Erde mit v=0 und beschleunigt innerhalb von ca. 0,8J irdischer Zeit bis 0,6c, dann fliegt er inertial (ca. 30° Neigung der Raumachse) bis kurz vor dem Zielplanet (Weltlinie P) und bremst wieder für ca. 0,8J ab. Am Zielplanet macht er keine Pause, sondern beschleunigt wieder wie gehabt und fliegt zurück zur Erde.
Die jährlich gezeichneten und sich kreuzenden Pfeile zeigen wie man die Zeit nach MD und LT abgelesen sein muss - identisch wie im ersten MD - s. dort Punkt 2, wie auch im symmetrischen MD.
In rot ist die Zeit des Erdlings (unbewegter Beobachter) und die entsprechenden roten Pfeile zeigen was er beim Reisenden SIEHT. In blau - die Zeit des Reisenden und die blauen Pfeile zeigen was er beim Erdling SIEHT.

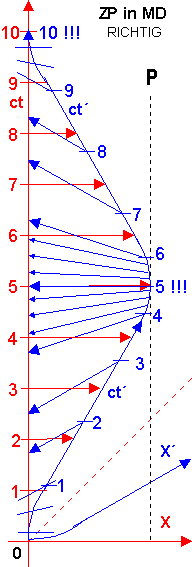1. Der Zeitverlauf von 0 (Start) bis Erreichen der Weltlinie des Zielplanets: Beim Start ist die Raumachse des Reisenden parallel zur Raumachse des Erdlings, mit zunehmender Beschleunigung neigt sich seine X´- Achse bis sie 30° erreicht (Inertialflug). Beim Abbremsen am P neigt sich seine X´-Achse stetig wieder zurück bis 0°, die ct´-Achse entsprechend bis 90° = parallel zur ct des Erdlings. Welche Uhr was zeigt und welcher Beobachter was im anderen System sieht, ist klar aus der Zeichnung zu entnehmen und jeder Zeit nachzurechnen. Mit zunehmender Geschwindigkeit erhöht sich Gamma, beim bremsen vermindert sie sich. Zuerst wird die Zeitskala des Reisenden gedehnt erscheinen, beim Bremsen umgekehrt. Genauso auch die Zeitachse des Erdling wird aus der Sicht des Reisenden erscheinen. Als der Reisende sich am Zielplanet befindet, sehen beide, der Erdling und Reisende, genau gleiche Zeit, wie auch Zeitdauer!!!

2. Der Zeitverlauf vom Zielplanet zurück zur Erde: Jetzt beschleunigt wieder der Reisende, seine Raumachse neigt sich wieder stetig bis 30°, jedoch jetzt in umgekehrter Richtung, entsprechend auch seine ct´-Achse. Die Zeitablesung erfolgt analog wie bei der Anreise. Bei der Ankunft auf der Erde ablesen und sehen beide Beobachter identische Zeit, nämlich 10 Jahren.

Nun, überprüfen wir das Gezeichnete mithilfe der LT, obwohl die LT bereits im MD enthalten ist, und besonders beim Bremsvorgang vor dem Ankunft am Zielplanet, um zu beweisen, dass die „zurückgebliebene“ Uhr des Reisenden gerade beim Bremsen wieder aufholt. Da es sich nur um Zeitvergleich zwischen zwei zueinander bewegten Systemen handelt, reicht die Formel t´= t/y, wobei y = Gamma = 1/sqrt(1-v²/c²); t´ sind die Zeiten des Reisenden, t sind die Zeiten des Erdlings. Um die Zeitentwicklung zu beurteilen, nehmen wir einen irdischen Zeitabschnitt zwischen Inertialflug (v=0,6c) und kurz vor Ankunft am Zielplanet (v=0,1c). t1 wählen wir vor der Bremsung = 4,2J und t2 = 4,9J.
Oder, dt = t2 - t1 = 0,7J und entsprechend berechnen wir jetzt dt´= t´2 - t´1.
y1(0,6c) = 1,25
y2(0,1c) = 1,005
t´1 = t1/y1 = 4,2/1,25 = 3,36J
t´2 = t2/y2 = 4,9/1,005 = 4,87J
dt´= t´2 - t´1 = 1,51J sind scheinbar beim Reisenden vergangen, während die irdische Uhr einen Zeitabschnitt von nur 0,7J zeigt. Das Gleiche sieht auch der Reisende beim Erdling.

Wie ist das im Rahmen der SRT, LT und Weltpostulat zu erklären: Das Beschleunigungsmanöver (Starten, Bremsen) kann man in unzähligen kleinen Zeitintervallen dt zerlegen, in denen die Geschwindigkeit als konstant betrachtet werden kann. In diesen dt haben wir also Inertialsysteme, wo auch die beobachteten Zeiten des anderen langsamer verlaufen (s. auch Einstein 1907). Bei jedem nachfolgenden Sprung in nächstes IS, wo Gamma einen anderen Wert hat, überschneiden sich, bzw. gehen auseinander die beobachteten, langsamer verlaufenden Differentialzeiten und beim Integrieren ergeben sich die scheinbar schneller laufenden Uhren des jeweils anderen. Oder, beim hochgepriesenen Inertialsystemwechsel wird eine Uhr scheinbar zurückbleiben oder vorrücken, bei nächster entgegengesetzten Beschleunigung wird sie die scheinbar „verlorene“ oder „gewonnene“ Zeit aufholen - s. auch unter VIII.
Dieser Zeitablauf ist auch im Prinzip auf der Zeichnung zu erkennen. Genauso kann man auch den scheinbaren Uhrzeitablauf während der Beschleunigung beim Rückflug berechnen und sehen, dass in der irdischen Zeitspanne von 0,7J beim Reisenden 1,51J vergehen, und dass jetzt jeder Beobachter eine vorgerückte Zeit beim anderen SIEHT. Befindet sich die Rakette wieder in Inertialflug, sieht jeder Beobachter den Uhrgang des anderen nachgehen.
Und das alles hat seine Richtigkeit, da Gamma nur eine trigonometrische Funktion wiedergibt, und die kleinste Winkeländerung bei langen Dreieckschenkeln eine große Änderung auf der ct-Achse bewirkt (RdG).

Ich habe absichtlich deutliche Beschleunigungsphasen, die eigentlich auch realistisch sind, genommen, so dass man genauer die Entwicklung der Neigung der Sichtachsen (Raum-, Gleichzeitigkeitsachsen) ablesen und nachvollziehen kann. Egal, ob die Reisedauer sogar mit Potenzen verlängert wird, bzw. die Beschleunigungsphasen sehr kurz gahalten werden, ändert sich absolut nichts im Prinzip, und diese richtige Darstellung bleibt konform mit der SRT und LT.
Es ist auch nicht anderes zu erwarten, nachdem bei Minkowski und LT keine bewegten Uhren real nachgehen.

IV. Längenkontraktion und die Folgen beim ZP

Folgendes bezeichnendes Zitat habe ich im Wikipedia ausgegraben, und es zeigt überdeutlich, dass einige Relativisten (Physik-Professoren darunter) nicht mal 2+2 zusammenrechnen und nicht mal mit zwei Inertialsystemen umgehen können, wenn es um die SRT geht:

„Aus der Sicht des Zwillings auf der Erde sind für Hin- und Rückweg jeweils 5 Jahre erforderlich. Der Faktor für die Zeitdilatation und die Längenkontraktion beträgt 0,8. Das bedeutet, dass der fliegende Zwilling auf dem Hinweg nur um 5x0,8=4 Jahre altert. Dieser erklärt sich diesen geringeren Zeitbedarf damit, dass die Wegstrecke sich durch die Längenkontraktion bei seiner Reisegeschwindigkeit auf 3x0,8=2,4 Lichtjahre verkürzt hat. Da nach seiner Einschätzung auf der Erde die Zeit auch langsamer verstreicht, scheint auf der Erde unmittelbar vor seiner Ankunft am fernen Stern lediglich 4x0,8=3,2 Jahre verstrichen zu sein. Während der Umkehrphase verstreichen aber auf der Erde seiner Ansicht nach zusätzlich 3,6 Jahre. Zusammen mit den 3,2 Jahren auf dem Rückweg sind also auch aus der Sicht des fliegenden Zwillings auf der Erde insgesamt 10 Jahre verstrichen, während er selbst lediglich 8 Jahre gealtert ist.“

Es ist harrsträubend, was für dilettantische Fehler sich in diesem Zitat verbergen. Sehen wir von der metaphysischen Aussage „Während der Umkehrphase verstreichen .... 3,6 Jahre“ ab und rekonstruieren die Situation in Detail:

Die Strecken: Aus der SICHT DES REISENDEN verkürzt sich die Strecke Erde-Zielplanet um Faktor 0,8. In welchem Inertialsystem (IS) befindet sich diese verkürzte Strecke? In seinem eigenen bestimmt nicht - diese Verkürzung wird immer im fremden IS beobachtet, nämlich in Erde-Zielplanet und beträgt 3LJ*0,8 = 2,4LJ. In welchem IS fliegt der Reisende? Wohl in seinem Raumschiff-Zielplanet-IS, wo sich nichts verkürzt, und nicht im fremden IS.

Die Zeiten: Aus der SICHT DES REISENDEN läuft die Zeit im fremden IS mit Faktor 0,8 langsamer. Oder, wie im Zitat angegeben, wenn er auf seine Uhr 4J abliest, SIEHT er im Erdsystem 3,2J. Er ermittelt seine Geschwindigkeit auf Grund der GESEHENEN Zeiten und Strecken im Erdsystem: v = s/t = 2,4LJ/3,2J = 0,75c!!! Da stimmt was nicht! Die Geschwindigkeit war doch 0,6c? Suchen wir den Fehler und rechnen mit der richtigen Geschwindigkeit (Invarianz der Geschwindigkeit). Die Strecke im fremden IS erscheint kontrahiert und beträgt 2,4LJ. Wenn er mit 0,6c fliegt, würde er bei Ankunft am Zielplanet folgende Zeit im Erdsystem sehen müssen: t = s/v = 2,4LJ/0,6c = 4J und nicht 3,2J . Wenn er im Erdsystem 4J sieht, was muss seine eigene Uhr vor Ort zeigen: t´= t/0,8 = 5J!!!

Höchst unglaubwürdig klingen auch die Aussagen des Autors dieser oben zitierten Publikation. Obwohl er mehrmals Scheinvorgänge bekundet: „Aus der Sicht“, „nach seiner Einschätzung “, „scheint auf der Erde“, „seiner Ansicht nach“ - proklamiert er gleichzeitig und bedenkenlos: „nur um 5x0,8=4 Jahre altert“, „die Wegstrecke sich ... verkürzt hat“, „er selbst lediglich 8 Jahre gealtert ist“.

Da 99% der Relativisten erhebliche Probleme mit der Zuordnung eines Vorganges in richtigem IS und entsprechendem Umgang mit ZD und LK vorweisen, werde mich bemühen in folgenden MD Klarheit zu schaffen.

Wiederholen wir die Grundsätze der SRT: Jeder Beobachter SIEHT in einem, sich in relativer zu ihm Bewegung befindenden IS die dortige Uhrzeit langsamer verlaufen und die dortigen Längen kürzer. Jeder Beobachter sieht in seinem eigenen IS keinerlei relativistischen Veränderungen. Und nochmals: Unter „SIEHT“ ist Messen mit Licht-, Funksignalen nach Einsteins Synchronisationsmethode gemeint und entspricht einer Anwendung der Lorentz Transformation. Die beobachteten Werte fallen von jedem IS symmetrisch aus - Gleichberechtigung der IS, Relativitätsprinzip. Dieser Hokuspokus ist für die Aufrechterhaltung der postulierten Invarianz der Lichtgeschwindigkeit notwendig.

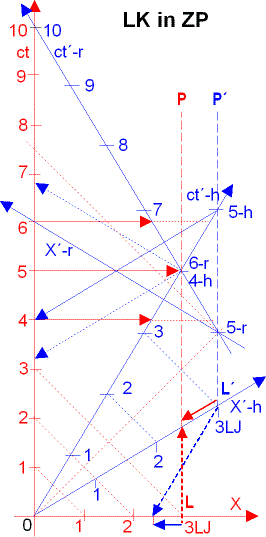
Sehen wir jetzt erneuert das Zwillingsparadoxon in einem MD, wobei jetzt auch die Längenkontraktion (LK) einbezogen wurde. Wie gehabt, ist in rot alles, was der unbewegte Beobachter (Erdling) sieht und in blau alles, was der bewegte Beobachter (Reisende) sieht.
ct´-h und X´-h für der Hinflug; ct´-r und X´-r für den Rückflug.

In einem MD zeigt die ct-Achse die Zeitverlauf und die X-Achse die räumliche Entfernung. Da die Einteilung der ct-Achse 1:1 der Einteilung der X-Achse, wo die Entfernungen in c*t angegeben sind, entsprechen muss, wird sie ct- und nicht t-Achse benannt. Das bedeutet, werden wir auf der ct-Achse 1cm für 1J eintragen, müssen wir auf die X-Achse 1cm für c*1J = 1LJ auch eintragen. Das gilt für beide IS - die Skala für ct´ muss auch 1:1 der X´-Skala entsprechen. Wie wir aus der Gegenüberstellung des symmetrischen MD gesehen haben, wird die Zeitskala des Bewegten aus der Sicht des Unbewegten gedehnt, obwohl die Uhren gleich laufen. Was ist mit der Raumskala? Sie muss genauso 1:1 gedehnt gezeichnet werden. Das 1:1 Skalen-Verhältnis beider Achsen ist mit 45° punktierten Linien dargestellt.

Betrachten wir die Längenkontraktionen: Denken wir uns der Abstand Erde-Zielplanet als einen Stab der Länge L, der in Ruhe die Länge 3LJ aufweist und auf der X-Achse 0 bis L entspricht. Lassen wir auch eine Kopie des Stabes im bewegten IS liegen (in der SRT wird diesen Stab Maßstab genannt). Wer wird was beobachten - s. auch ganz oben das erste Minkowski-Diagramm. Der Erdling wird den bewegten Stab verkürzt wahrnehmen = L/y = 3LJ/1,25 = 2,4LJ - die Verkürzung zeigt der rote Pfeil auf der X´-Achse. Der Reisende wird den ruhenden Stab auch verkürzt wahrnehmen = L´/y = 3LJ/1,25 = 2,4LJ - seine empfundene Verkürzug zeigt der blaue Pfeil auf der X-Achse. In seinem eigenen System sieht jeder Beobachter eine unveränderte Länge.

a) Die Weltlinie des Zielplanets P befindet sich aus Sicht des Erdlings auf 3LJ und auf seiner X-Achse. Die Weltlinie des Zielplanets P´ befindet sich aus Sicht des Reisenden genauso auf 3LJ und auf seiner X´-Achse. Wie wir sehen, verlaufen beide Weltlinien im Diagramm versetzt. Der Reisende hat die Strecke in seinem IS zu befahren und nicht die Strecke im Erdsystem.
Jetzt glaube ich ist auch die Situation mit den „herausragenden“ ct´-Achsen bei der Gegenüberstellung des symmetrischen MD verständlich geworden.

Jetzt erkennen wir, was die Relativisten im „falschen MD” verbrochen haben: Sie ließen den Reisenden umkehren, bevor er den Zielplanet erreicht hatte. Auch eine Überprüfung nach LT bestätigt den Fehler - die Wende wurde bei x´= 2,4LJ vollzogen. Aus Unkenntnis entstehen immer Wunder, wie z.B. Zeitsprünge und junggebliebene Zwillinge, vom ewig lebenden Organismus in geschüttelter Einsteins Schachtel ganz zu schweigen.

In diesem MD fliegt der Reisende auf der ct´-h bis er die Weltlinie des P´ (5-h) erreicht und von dort aus auf der ct´-r (5-r) bis zur Erde. Das, was als Zeitsprung aussieht, ist keiner, da wie ersichtlich ist, befand sich der Reisende nur zur Zeit 5,000J am gleichen Ort P´. Was hier verrückt spielt, sind nur die SICHTEN der beiden Beobachter, und das ist nur eine graphische Erscheinung, da die Vorgänge während der Beschleunigungen nicht eingezeichnet sind.
Man könnte das Hin- und Rück-MD auch so andocken, dass bei der Ankunft und Anreise am Zielplanet keine versetzten ct´-Achsen auftreten, dann muss man jedoch die ct-Skalen für hin und zurück entsprechend so verlängern, dass die Hin-Skala bei 6,25J aufhört, dafür die Rück-Skala bei 3,75J anfängt. In Prinzip bleibt alles gleich.

b) Diese Feststellung - die Weltlinie des Zielplanets verläuft für den Reisenden in einem MD auf einem Abstand von L*Gamma - kann man jederzeit mittels Einsteins-Synchronisationsmethode überprüfen. Sendet der Reisende zum Zeitpunkt 1J einen Lichtstrahl (Kugelblitz) zur Erde und Zielplanet (P´), wird er beide Reflektionen bei 4J Lokalzeit zurück empfangen. Die Rechnung: 3J Lichtlaufzeit geteilt durch 2 = Lichtlaufzeit bis Erde und Zielplanet je 1,5J. Folglich befand er sich zum Zeitpunkt der Reflexion (2,5J seiner Zeit) auf 1,5LJ von beiden Bezugspunkten entfernt = alles stimmt. Nun, würde das Lichtsignal nicht an P´, sondern an P reflektieren, wird er feststellen, dass alles bis zur Erde wie oben stimmt, d.h. 1,5LJ Entfernung und v=0,6c. Nach der Reflexion an P bekommt er jedoch einen Abstand von 1,2LJ. In dem Fall kann man sich selbst eine Rechtfertigung aussuchen: Entweder ist der Abstand nur in einer Richtung „geschrumpft“, oder die Lichtgeschwindigkeit nur in einer Richtung 1,25c wäre.

Nachdem geklärt wurde, wer welche Längenkontraktion sieht und wer in welchem IS sich tatsächlich bewegt, ist auch der Argumentation, bei der s.g. Myonen-Zeitdilatation mit „gesehenen“ kontrahierten Strecken “erklärt” wird, den Boden entzogen. Dass ein Myon im Erdsystem eine verkürzte Strecke bis Erdboden sieht, bedeutet nicht, dass es diese fremde Strecke durchfliegt, sondern seine eigene und unverkürzte. Siehe auch die Berechnungen in der Anlage unter V - dort Punkt 5.

Es ist erschreckend, wenn ausgebildete Physiker behaupten, ein Reisender soll die scheinbar verkürzte Strecke im fremden Inertialsystem real befahren.

Anmerkungen: Jetzt ist die Zeit auch einige Feinheiten, die vielleicht nur sehr wenigen Lesern auffallen werden, zu klären. Beim symmetrischen und dazugehörigen R- und B-Diagramme, habe ich die Zeitskala der Erde absichtlich nicht angegeben. Mir erschien das für zu verfrüht, solange die Längenkontraktion und die entsprechenden Skalenverschiebungen noch nicht behandelt wurden, und hätte den Leser nur verwirrt. Um das Verstehen des Prinzips eines Minkowskidiagramms zu erleichtern, müsste ich eine Reihenfolge einhalten. Nachdem bereits den kompletten Stoff durchgearbeitet wurde, kann sich jeder die Verschiebung der Erdzeitskalen, gerade in der Mitte bei 5J, bzw 0J vorstellen. Bzw. sollte man in diesem symmetrischen MD die Erdzeitskala als angegeben betrachten, dann werden die ct-Achsen und Skalen der Zwillinge genauso ein Stückchen nach Außen „ragen“ und sich überschneiden.
Die Weltlinie des Zielplanets aus der Sicht des Reisenden beim MD mit Beschleunigungsphasen wurde aus obigen Gründen nicht eingezeichnet, spielte dort auch keinerlei Rolle. Sie würde genauso „gekrümmt“ verlaufen - beim Start am gleichen Ort, wie die Weltlinie aus Erdsicht, dann mit zunehmender Geschwindigkeit wird sie sich bis auf L*Gamma (0,6c) entfernen, dann bei Bremsung krümmt sie sich zurück und wird bei Ankunft mit der Erdsicht-Weltlinie zusammenfallen. Beim Rückflug geschieht das Gleiche.

V. Anlage: Die Berechnungen nach der Lorentztransformation

VI. Nachtrag:

1. Ankoppeln von mehreren Minkowski Diagrammen.

Wegen der Vergleichbarkeit mit etlichen MD, die das Zwillingsparadoxon darzustellen versuchen, schrieb ich bislang von EINEM MD, was an sich falsch ist. Es handelte sich um EINE Zeichnung, in der mehr als ein MD angekoppelt wurden.
Ein Minkowski-Diagramm ist nur für eine einzige relative, gleichgerichtete und inertiale Bewegung zweier Körper zueinander bestimmt. Ob man dann im Diagramm die Weltlinien beider Körper symmetrisch darstellt, oder die eine davon als ruhend betrachtet, ist frei zu wählen und führt zu keinerlei Asymmetrien. Problematischer wird es, wenn ein Richtungs- oder Geschwindigkeitswechsel mitgezeichnet werden soll. Bei jedem Richtungs- oder Geschwindigkeitswechsel entsteht ein neues Diagramm. Um den gesamten Ablauf grafisch darzustellen, kann man diese jetzt zwei, oder mehr Diagramme ankoppeln. Das geht ohne weiteres, solange man weiß, was was bedeutet und wie das zu bewerkstelligen wäre. Die einfachste Art zwei oder mehr Minkowski-Diagramme anzukoppeln ist, wenn die Weltlinien symmetrisch eingezeichnet werden – das ist der Fall bei a) in der Zeichnung unten. Hier sehen wir das uns bereits bekannte ZP-Diagramm, oder zwei Körper entfernen sich inertial voneinander (0 bis 3 s oder Lj) und anschließend nähern sie sich bis zu erneuertem Treffen (3 bis 6 s oder Lj). Mit H (Hinreise) ist das erste MD und mit R (Rückreise) das zweite MD benannt. Die schwarze, wagrechte, punktierte Linie trennt die einzelnen MD voneinander. In den Diagrammen sind die Sichtlinien beider Beobachtern kurz vor und kurz nach 3 eingezeichnet, wobei man nicht vergessen darf, dass die Sichtlinien kurz vor 3 noch zu MD-H und kurz nach 3 zu MD-R gehören. Der Winkel der Achsen zueinander entspricht v = ca. 2/3c. Nun, zeichnen wir die Minkowski Diagramme so, dass Rot als ruhend und Blau als der bewegte erscheinen und versuchen die entsprechende MD aneinander anzukoppeln – dass geschieht in b) und c).

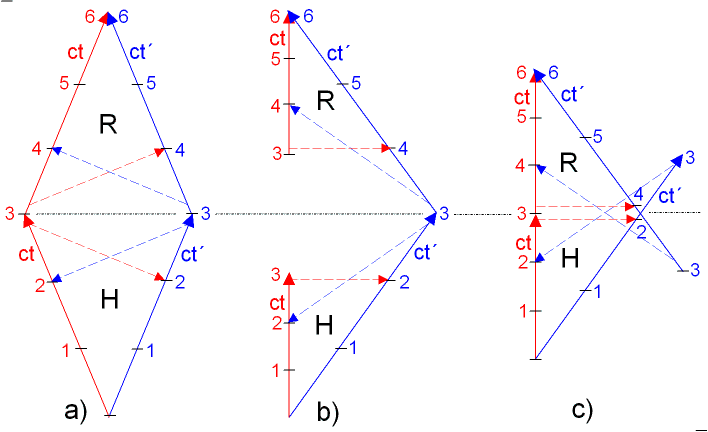
Alle drei MD – a), b) und c) sind absolut identisch und zeigen die gleichen Bewegungen und Körper. Diese je zwei MD, wo Rot als ruhend dargestellt ist, können wir aber nicht lückenlos oder ohne Überlappung von zwei Achsen ankoppeln, wie der Fall beim symmetrischen MD war. Wir können entweder an die ct oder an die ct´ Achse andocken. In b) ist an ct´ angedockt – da entsteht aber zwangsweise eine Lücke zwischen beiden ct-Achsen. Diese Lücke hat absolut keine Bedeutung und hat mit Zeitsprüngen oder dergleichen nichts zu tun. Würde man bestimmte Lichtstrahlen betrachten wollen, die genau in diese Lücke eintreffen, dann muss man einfach entweder die untere ct nach oben, oder die obere ct nach unten verlängern und maßstabgetreu die Skalenwerte eintragen. In c) ist an ct angedockt – das MD, das wir schon kennen – zwangsläufig müssen sich hier die ct´-Achsen schneiden und überlappen – das hat genauso nichts zu bedeuten, wie im Fall b), solange man die herausragenden Stücke der ct´-Achsen nicht vergisst und bei jeder Betrachtung einbezieht.

An dieser Stelle ist angebracht etwas aus der Elementarphysik einzufügen, da wie ich aus vielen Diskussionen erfuhr, haben einige, darunter ausgebildete Physiker, damit erhebliche Probleme. Die Spezielle Relativitätstheorie (SRT), unabhängig davon, ob es sich um Einsteins- oder Minkowskis-SRT handelt, betrifft nur Relativbewegungen zwischen zwei Körper. Man kann den einen Körper (Beobachter) als ruhend und den anderen als bewegt betrachten, um bestimmte Sachverhalte verständlicher zu machen, zu vereinfachen, das darf aber auf keinem Fall wörtlich genommen werden und als eine relative Zuordnung zu irgendeinem globalen Bezugssystem verstanden werden. In der SRT sind beide Körper, Beobachter, Inertialsysteme völlig gleichberechtigt und unabhängig von einem Äther oder mangelhaftem menschlichen abstrakten Denken. Was hat das zu bedeuten? - Dass die relative Bewegung & Geschwindigkeit immer dieselbe ist und das zu jeder Zeit. Es spielt überhaupt keine Rolle, ob der eine Körper unsere Erde und der andere eine Rakete oder sogar ein Elementarteilchen ist. Es spielt auch keine, absolut keine Rolle, ob im Verlauf der Zeit, der eine oder andere Körper seine Richtung oder Geschwindigkeit ändert – es ändert sich dann die relative Geschwindigkeit gleichermaßen für beide Körper. Dass in so einem Fall, der eine Körper eine Beschleunigungskraft spürt, hat mit der relativen Geschwindigkeit zwischen beiden nicht das Geringste zu tun. Und, die relativistischen Effekte – Zeitdilatation und Längenkontraktion entstehen ausschließlich aufgrund und proportional der relativen Geschwindigkeit. In der SRT gibt es keine „bewegten“ oder „unbewegten“, sondern nur „zueinander bewegten“ Beobachter. Wer diesen Grundsatz der Physik nicht verstanden hat, hat auch in der SRT nichts verloren.

Daraus ist ersichtlich, dass, um Fragestellungen zu behandeln, wo mehr als ein MD und ein Ankoppeln notwendig erscheint, am besten symmetrische Minkowski Diagramme anzuwenden wären. Die nur scheinbar bevorzugten Darstellungen, wo die ct-Achse des einen Beobachters senkrecht verläuft, verleiten offensichtlich viele Betrachter dazu, diesen Beobachter als tatsächlich unbewegt zu betrachten und unbewusst einen Äther, oder egal auch was absolutes, zu unterstellen. Und das ist oft der Fall, wenn naive Relativisten einen dritten, nicht an der Bewegung teilnehmenden Beobachter hinstellen.

Wenn man jetzt auch das erste Postulat der SRT, nämlich die Invarianz der Lichtgeschwindigkeit, geschweige denn das Relativitätspostulat, dazu zählt, wird man überdeutlich begreifen, dass in der SRT ein Zwillingsparadoxon nicht existieren kann und darf – es handelt sich nur um einen Einsteins-Denkfehler.

Der Prüfstein, oder Messlatte, ob jemand die SRT verstanden hat, ist das Zwillingsparadoxon – d.h. wer behauptet, dass laut SRT einer der Zwillinge jünger oder älter nach der Reise geblieben sein soll, der hat die SRT nicht mal im Ansatz verstanden.

2. Beschleunigungen in Minkowski Diagrammen:

Um zu verstehen, was da während einer Beschleunigung in Rahmen der SRT und in Minkowski-Diagrammen vor sich geht, habe ich folgende Zeichnung angefertigt. In a) wird eine völlig symmetrische Reise behandelt – wie ich oben angegeben habe, ist für solche Fälle, wo mehrere MD anzukoppeln sind, die symmetrische Darstellung am besten geeignet. Nicht vergessen – alle Bewegungen zwischen zwei Körper verlaufen immer mit identischer relativen Geschwindigkeit zueinander! Es spielt überhaupt keine Rolle, ob nur der eine und welcher der Beobachter, oder beide gleichzeitig, tatsächlich beschleunigt wurden.

Die Beschleunigungen – zuerst positiv 1 bis 3 und dann negativ 4 bis 6 (Bremsung) sind in kleineren Abschnitten unterteilt. Zwischen den Abschnitten, die für sich allein Inertialbewegung entsprechen, sind doch leichte Knicke der ct-Achse übriggeblieben. Sie sind nichts andere als die Andockstellen der einzelnen MD. Gezeichnet sind die Sichtlinien nur des einen, linken Beobachters. Die Sichtlinien des anderen fallen genauso aus und würden nur die Zeichnung belasten. Die Abschnitte habe ich abwechselnd in rot und blau gezeichnet, so dass man die entsprechenden Sichtlinien besser verfolgen kann. Die Sichtlinien sind paarweise – eine am Anfang und eine am Ende jedes Abschnittes und entsprechend der rel. Geschwindigkeit in diesem Abschnitt - mit punktierter Linie dargestellt.

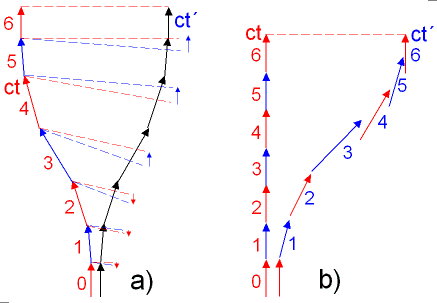Fangen wir bei Ende Abschnitt 2 und Anfang Abschnitt 3 – dort kann man eher die Linien unterscheiden – die rote Ende-Linie des Abschnitts 2 hat eine kleinere y (Gamma) als die blaue Anfang-Linie von 3 und trifft ct´ höher (später) als die blaue von 3. Bei der Übergang zwischen 2 und 3 entsteht zeichnerisch ein Sprung der beobachteten Zeit bei ct´ rückwärts. Dieser Zeitsprung rückwärts hat keinerlei physikalische Bedeutung – er entstehet nur auf der Zeichnung, da auch der Knick zwischen den Abschnitten einer instantanen, unendlichen Beschleunigung entspricht. Bei realer stetigen Beschleunigung wird der Beobachter nur feststellen, dass die Zeit beim anderen Körper viel langsamer als bei Inertialbewegung verläuft. Diese Rücksprünge entstehen auch bei den Übergängen zwischen 0 und 1; 1 und 2 – jedoch mit kleinerem Wert.
Am Ende von 3 beginnt die Bremsung – dort bei den Knickpunkten entstehen genauso „Zeitsprünge“, jetzt aber vorwärts, da der nächste Abschnitt eine kleinere Gamma aufweist. Diese „Zeitsprünge in der Zukunft“ haben, wie oben, genauso keinerlei Bedeutung – sie zeigen nur, dass bei einer realen stetigen negativen Beschleunigung, der Beobachter eine viel schneller verlaufende Zeit im anderen System sehen, messen wird. Würden wir die Sichtlinien nur eines Abschnittes verfolgen, werden wir auch feststellen, dass sie bei Beschleunigung und Bremsung immer eine kleinere Zeitspanne auf der ct´-Achsen abschneidet – das ist die normale Zeitdilatation während der Inertialbewegung. Betrachten wir jetzt die Werte der „Zeitsprünge“ – in rot und nach unten - rückwärts; in blau und nach oben – vorwärts: Die Winkel zwischen den Sichtlinien sind gleich, da auch die Beschleunigungen (Knickpunkte) identischen Wert haben, die Abstände zwischen den Beobachter steigen jedoch mit der Entfernung und somit steigen auch die Werte der „Zeitsprünge“. Am Ende – Phase 6 – unbewegt zueinander - zeigen die Uhren wieder die gleichen Werte. So wird gerechnet: Die drei relativ kleinen Rückwärtszeitsprünge plus die inertiale ZD der gesamten Reise minus die drei relativ große Vorwärtszeitsprünge ergeben am Ende eine Zeitdilatation = 0. Alles, absolut alles, kann man auch mithilfe der LT nachrechnen und sich überzeugen, dass ein Zwillingsparadoxon in der SRT nichts zu suchen hat.

In der zweiten Zeichnung b) habe ich in etwa das Gleiche, wie in a) gezeichnet, jedoch jetzt den linken Beobachter als „unbewegt“ dargestellt. Bevor ich aber die entsprechenden Sichtlinien einzeichne und dazu jede Menge Erklärungen hinzufüge, warum diese und jene Skala so und so verlängert sein muss, lasse es lieber, und die Zeichnung soll nur zeigen, wie in etwa die ct´ -Achsen angeordnet sein sollen – nicht vergessen, es handelt sich um insgesamt 7 MD, die angedockt sind. Ich hoffe, man kann jetzt besser verstehen, was oben in der Zeichnung („ZP in MD RICHTIG“ – Abschnitt III) vor sich geht - s. auch unter VIII.

3. Auch die hartgesottensten Relativisten platzen bei folgender Aufgabe: Es soll ein Minkowski Diagramm samt Überprüfung laut LT nur für die Rückreise aufgestellt werden, und das so, dass alle SRT-Postulaten erfüllt sein müssen.
Wir haben, wie oben, zwei Planeten (Erde und Zielplanet), die auf Abstand von 3Lj unbewegt zueinander sich befinden. Die Uhren auf beiden Planeten laufen synchron (kein Problem). Am Zielplanet vorbei fliegt ein Raumschiff in Richtung Erde und mit v relativ zu den Planeten gleich 0,6c. Direkt vor Ort am Zielplanet übernimmt das Raumschiff die Zeit des Zielplanets – zur Vereinfachung stellen wir alle Uhren auf 0. Zeichnen und berechnen wir jetzt, was in diesem Augenblick die Erd-Beobachter in Raumschiff-IS SEHEN und umgekehrt.
y ist bei v (0,6c) = 1,25; c = 1; x = 3Lj. Ereignis bei t = 0 und auf der Erde.
x´ = [-x - (-v)*t]*y = -3,75Lj in Erdeinheiten (t = 0)
Obwohl das Schiff sich beim Zielplanet befindet, d.h. auf 3Lj Entfernung, sehen (messen, berechnen) die Erdbeobachter die Startkoordinaten weiter entfernt.
t´ = [t - (-v)*x]*y = 2,25J – diese Zeitangabe würden die Erdbeobachter auf der Raumschiffsuhr dann sehen, wenn das Raumschiff bei x´=3,75Lj Entfernung aber bei t´= t = 0 gestartet würde. Mit einer räumlichen Verschiebung der x´-Startkoordinaten, hier von 3LJ auf 3,75LJ, ist auch eine zeitliche Verschiebung der ct´-Koordinaten verbunden (RdG) und die ist nichts andere, als die Flugzeit für diese 0,75LJ und ist gleich 1,25J, die in der Gleichung berücksichtigt werden müssen. So bekommen wir für t´= 1J. Und das werden die Erdbeobachter auf die Raumschiffsuhr sehen, als das Schiff sich beim Zielplanet befindet – d.h. sie werden meinen, dort ist bereits ein Jahr vergangen, obwohl das Schiff sich gerade beim Zielplanet befindet und soeben seine Uhren auf 0 gestellt hat.
Nachdem die “gesehene” Startkoordinaten bestimmt wurden, haben wir auch die nötige Symmetrie (Relativitätsprinzip) zwischen beiden Inertialsysteme hergestellt, somit wird auch die Raumschiffbesatzung die gleiche Beobachtungen in Bezug auf die Erde machen.

Die zwei einzig möglichen grafischen Darstellungen (MD) sind unten in E (links), wo die Erde als Basis und P (rechts), wo der Planet als Basis genommen ist, gezeichnet. Beide MD sind identisch, bei beiden ist ersichtlich, dass die Erd- bzw. Planetbeobachter den Start-, bzw. Zielort und die Start-, bzw. Zielzeit im Raketensystem anders als die tatsächlichen MESSEN, SEHEN, EMPFINDEN. Genauso ist der Fall bei den Raumschiffsbeobachtern – sie sehen auch die Erdkoordinaten verschoben. Das ist die Folge der angenommenen Invarianz der Lichtgeschwindigkeit und ist unter der Bezeichnung „Relativität der Gleichzeitigkeit“ (RdG) bekannt.

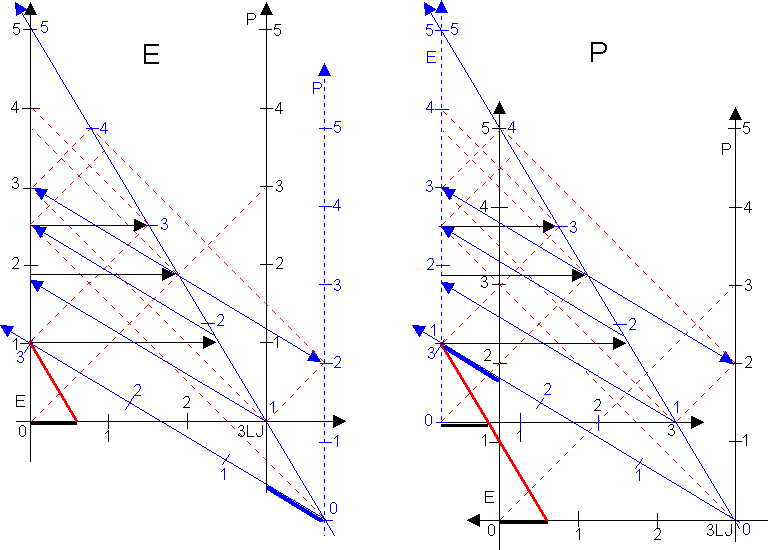
Jetzt möchte ich mal sehen, wo die oberschlauen Relativisten, besonders in MD links (E) etwas abschneiden würden, um die Zeit des Raumschiffs während des Rückfluges kürzer erscheinen zu lassen!

VII. Es kursieren einige ZP-Darstellungen (Drillings-Problem), die die Fragen nach den Beschleunigungen umzugehen versuchen, indem sie zwei Raumschiffe, die nur bei einem Vorbeiflug an die Erde und gegenseitig beim Ziel, sich die Zeitangaben übertragen. Erneuert ist hier die Naivität und Unkenntnis der Verfasser solcher Gedankenexperimente zu erkennen. Sie glauben, die Uhren gehen tatsächlich nach, und am s.g. Wendepunkt eine „zurückgebliebene“ Zeit in anderen Raumschiff übertragen wird. Wie wir das Problem tiefgründig untersucht haben, zeigen die „bewegten“ Uhren vor Ort eine reale und nicht dilatierte Zeit, nur diese Zeitangabe kann auch weitergegeben werden und nicht die Scheinuhrzeit aus irdischer Sicht. D.h. am Wendepunkt in unserem Zahlenbeispiel wird die Zeitangabe 5,00J herüber “geworfen” und keine 4J.

Bei solchen Publikationen, wo mit getürktem MD eine tatsächliche Zeitdilatation vorgegaukelt wird, sind häufig auch Folgerungen als angeblich weitergehende Bestätigungen anzutreffen - s. z.B. in Wikipedia - Zwillingsparadoxon. Es wird ein falsches MD gezeichnet, in dem Lichtstrahlen zu bestimmten Zeitpunkten hin und her geschickt werden. Nun, so was nennt man Zirkelschluss, da der Zeitablauf des Bewegten bereits „dilatiert“ eingezeichnet wurde. Ist ja kein Wunder, dass dann nach Doppler-Effekt oder nur Zeitmitteilungen , genau das herauskommt, was schon im MD fälschlicherweise als existent vorgegeben wurde.

VIII. Nachdem wir das Zwillingsparadox auch in einem Minkowski-Diagramm entlarvt haben, widmen uns einer anderen falschen Behauptung betreffend ZP, nämlich die Beschleunigungen, denen angeblich nur der eine Beobachter (der Reisende) ausgesetzt sein soll.

Überprüfen wir die Beschleunigungen, die berechtigt für einen veränderten Gang von Uhren, auch ohne irgendwelche RT, in Betracht gezogen werden:
Der Reisende beschleunigt mit, sagen wir, g . Innerhalb ca. eines Jahres wird er c erreichen, dann fliegt er inertial (keinerlei Beschleunigung) 3 Jahre lang, dann bremst er mit g bis v = 0; am Zielplanet beschleunigt er wieder mit g usw. bis er wieder auf der Erde ist. Ich könnte auch mit wesentlich höherer Beschleunigung operieren, bringt aber nichts, da der Reisende laut Relativitätstheorie bis max. c fliegen darf, und größere Beschleunigungen werden entsprechend dann kürzer dauern, was sogar ein Einstein herausfand.

Rechnen wir nach: Der Reisende beschleunigt mit g insgesamt 4 Jahre lang und fliegt inertial 6 Jahre. Nun, da Albert in seiner Relativitätstheorie postulierte, dass bei Beschleunigung die Zeit langsamer verlaufen soll und dass bei Inertialbewegung jedes Inertialsystem (IS) gleichberechtigt wäre, d.h. die Zeit in so einem System verliefe gleich, wie in jedem anderen IS (Relativitätsprinzip), was wir auch in einem MD bewiesen haben, folgt, dass nur während einer Beschleunigung die Uhrzeit in diesem beschleunigten Bezugssystem langsamer verläuft. Erstaunlicherweise hat aber der gleiche Albert Einstein in der gleichen Theorie postuliert, dass Beschleunigung und Gravitation identisch sein sollen, oder, ob mit g beschleunigt, oder mit g auf der Erde „kleben“, ist egal - die Uhrzeit in beiden Situationen verliefe gleich.

Was ist jetzt mit dem Erdling, der ständig und das 10 Jahre lang ununterbrochen mit g beschleunigt war?
Oder, da der Reisende nur 4 Jahre, dagegen der Erdling aber 10 Jahre mit g beschleunigt wurde, ergibt sich nach der gleichen Theorie, dass der Erdling wesentlich jünger als der Reisende geblieben sein müsste, und das, je länger die Reise, desto junger.

Man könnte natürlich mit fingiertem Zwilling, der schwerelos irgendwo im All schwebt und auf seinen Brüder wartet, argumentieren. Ja, dann wäre der Reisende laut ART scheinbar etwas jünger, nicht aber nach den Einsteins Vorgaben. Was würde man noch erfinden, um den Einsteins Fehler zu vertuschen?

Aber gut, bleiben wir dabei und beachten nur die Beschleunigungen. Betrachten wir exakt nach der Relativitätstheorie das, was wir bereits unter III und VI (2) in einem Minkowski-Diagramm über die Beschleunigungsphasen herausgefunden haben:

1907 in „Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen“ – Kapitel V, §§ 17,18,19 (Jahrbuch d. Radioaktivität u. Elektronik IV S. 411) erweitert Einstein die SRT und bezieht auch beschleunigte Bezugssysteme und Gravitation mit ein. Zusammen mit der Forderung über eine Gleichheit zwischen träger und schwerer Masse, wurden in dieser Arbeit die Grundlagen der späteren „Allgemeine Relativitätstheorie“ (ART) gelegt.

Die Zeitdilatation in einer Beschleunigungsepoche wird hier analog den ursprünglichen Bestimmungen der SRT von 1905 mit den „so gerichteten Uhren“ während infinitesimaler Zeitabschnitte definiert. Das bedeutet, eine Uhr sollte diejenigen Zeitgang in so einer winzigen Zeitspanne aufweisen, der der relativen augenblicklichen Geschwindigkeit zwischen zwei Inertialsystemen S und S´ entspricht. Ist ja auch logisch – bei v relativ = 0 laufen beide Uhren gleich, bei v läuft U´ langsamer als U. Bis v erreicht ist (Zeitdauer), läuft also U´ stetig langsamer und langsamer. Genau das Gleiche geschieht auch mit der Längenkontraktion – währen der Beschleunigungsphase werden die Abstände, Längen im Fremdsystem immer kürzer und kürzer. Nach dieser Überlegung müsste eine Zeitdilatation (Uhrgang) vom Wert und Zeitdauer der Beschleunigung abhängen. Die Zeitdauer hat Albert aber unterschlagen und nur den Wert der Beschleunigung als bestimmend postuliert.

Jetzt taucht aber das Problem auf: Wird das „bewegte“ System S´ abgebremst, so dass es nach diesem Bremsvorgang relativ zum S wiederum unbewegt ist, läuft dann die Uhr U´ erneuert synchron mit U. Entsprechend werden auch Abstände, Längen, in, oder aus beiden Inertialsystemen betrachtet, identisch. Die einzig mögliche Folgerung liegt auf der Hand: Während des Bremsvorganges muss die bewegte Uhr U´ schneller als die unbewegte Uhr U laufen . Eine Bremsung ist jedoch genauso eine Beschleunigung – es kommt heraus, dass bei Beschleunigungsvorgängen eine bewegte Uhr langsamer oder schneller laufen wird. Weitergedacht, wird die Verlangsamung des Uhrganges während der positiven Beschleunigung mit dem Voreilen während der negativen Beschleunigung exakt kompensiert.

Andere Ursachen einer Zeitdilatation in Beschleunigungsphasen hat Einstein in der o.a. Arbeit ausgeschlossen – s. S. 455 unten – d.h. weder physikalische, noch durch IS-Wechsel bedingte kommen für die Zeitdilatation in Frage.

Die Folgerungen dargestellter Überlegung sind für die Einsteinslogik vernichtend:

a) Betreffend das Zwillingsparadoxon, sind alle Behauptungen, die Beschleunigungsphasen als Ursache einer realen Zeitdilatation annehmen, irrelevant.
Die Argumentation Einsteins in „„Dialog über Einwände gegen die Relativitätstheorie“ v. 1918 kann man nur als Unfug bezeichnen. Dort hat er die auftretenden positiven und negativen Beschleunigungen gleichgestellt.

b) Das Äquivalenzprinzip Einsteins, Beschleunigung mit Gravitation gleichzusetzen, erweist sich als unzutreffend. Die relativistischen Effekte bei einer Beschleunigung sind also von der Art der Beschleunigung, negativ oder positiv, abhängig und entgegengesetzt. Die Gravitation ist aber einseitig, dort gibt es keine positive oder negative Beschleunigung. Versucht man die Gravitation durch eine Beschleunigung zu beschreiben, dann muss man sich für die eine Art der Beschleunigung entscheiden. Einstein hat nur die positive Beschleunigung betrachtet. Mit gleichem Recht kann man aber auch mit einer negativen Beschleunigung vergleichen, ist sogar, der Ableitung aus der SRT folgend, zutreffender. Ein mitbewegter Beobachter kann ohne Vergleich zur Umwelt nicht entscheiden, um welchen Art der Beschleunigung es sich handelt. Eine mitbewegte Uhr noch weniger – wie soll dann diese Uhr laufen – schneller oder langsamer???

Ein Beobachter kann nur relativ zu einem Inertialsystem annehmen, beschließen, postulieren, ob es sich um positive oder negative Beschleunigung handelt. Positiv oder negativ ist also immer relativ, die Beschleunigung an sich jedoch immer absolut.

Für einen Inertialbeobachter muss eine, sich in freiem Fall befindliche Uhr langsamer als eine, die an der Erdoberfläche frei zu fallen gehindert wird, laufen. Hindern, um frei zu fallen, bedeutet nichts anderes, als dauerhaft gebremst zu sein.

Wenn man auch die, von Einstein „vergessene“, Zeitdauer der Beschleunigung dazu zählt, müsste eine Uhr z.B. auf der Erdoberfläche fortwährend schneller und schneller bis in die Unendliche laufen.

Die Ergebnisse:

1. Nach Einsteins Meinung und nach seiner SRT soll der REISENDE JÜNGER zurückkommen.

2. Nach SRT, LT und Minkowski bleiben beide GLEICH ALT.

3. Nach Einsteins Theorie (ART) kann nur der REISENDE ÄLTER zurückkommen.

Das Zwillingsparadox bleibt ein Paradox und keinesfalls Paradoxon. Würde man diese unhaltbare Einsteins Aussage zurückverfolgen, wird man auch feststellen, dass auch seine Idee mit den “so gerichteten Uhren” nichts taugt. Nicht zufällig wird heute die SRT mit Poincaré & Minkowski-Vierervektor und Minkowski-Raumkrümmung den Studenten vorgestellt. Von Einsteins Originalarbeit „Zur Elektrodynamik bewegter Körper“ wird kaum was, außer paar Sprüche, gelernt.

IX. Wie kam es zu diesem blamablen Einsteins Fehler?

In §2 seiner Arbeit „Zur Elektrodynamik bewegter Körper“ von 1905 übernahm Einstein die Vorstellungen von Poincaré, die eine Uhrensynchronisation in einem Äther beschreiben. Die Poincarés Idee von der Ununterscheidbarkeit zwischen bewegten und unbewegten Beobachtern im Äther, verleitete Einstein den Äther als nicht notwendig und die Inertialsysteme als gleichberechtigt zu betrachten - somit auch das Relativitätsprinzip in der SRT einzubauen. Nun gut, aber sein nur angenommen ruhendes K-IS war nichts anderes, als ein tatsächlich in einem Äther ruhendes IS und das fremde k-IS nichts anderes als ein tatsächlich in einem Äther bewegtes IS. Er schreibt selbst: „ Seien im „ruhenden“ Raume zwei Koordinatensysteme“. Es ist klar, dass nach einer Poincaré-Synchronisation (heute als Einsteins Synchronisationsmethode bekannt) die bewegten Uhren so verstellt werden, dass sie tatsächlich langsamer als die ruhenden gehen müssen. Bislang also nichts neues und alles entsprach Lorentz-Poincaré Theorie und einer Bewegung in einem Äther. Das neue von Einstein jedoch war, dass er aus Sicht des bewegten IS die Ätherkonstellation wechselte und jetzt dieses, ursprünglich bewegtes IS als das „ruhende“ deklariert wurde. Entsprechend fängt alles von neuem an, und jetzt werden die anderen Uhren verstellt. Oder, Einsteins Idee unterschied sich von Lorentz-Poincaré dadurch, dass jetzt, statt einen absoluten, einen wechselnden und an jedem beliebigen IS anhaftenden Äther postuliert wurde. Über die Unsinnigkeit solcher Vorstellung brauchen wir hier nicht zu diskutieren. Es geht nur darum, dass bei Einstein die Uhren in fremden IS immer die verstellten waren und dass sie dann auch tatsächlich, nicht nur aus der Sicht vom fremden IS, langsamer liefen . Begeistert von seiner Idee vergaß er gleich, dass es sich immer um ein Paar verstellte Uhren handelte und sprach über nur eine „so gerichtete Uhr“. Paar Sätze danach vergaß er auch das Adjektiv „so gerichtete“ und präsentierte eine Wunderuhr, die sich selbst, in Abhängigkeit von der relativen Geschwindigkeit zu dem bevorzugten IS, so verstellte, dass die bewegten Beobachter auch eine Lichtgeschwindigkeit gleich c messen würden. Paar Sätze weiter vergaß er auch noch, dass es sich nur um Uhren handelte und sprach schon von Zeit.

In seinem Kopf ist offensichtlich nur die Vorstellung von tatsächlich langsamer gehender bewegten Uhr geblieben, ohne zu überlegen, dass eine Bewegung immer eine Relation braucht, und in Abwesenheit von einem Äther nur die Relativgeschwindigkeit zwischen beiden Inertialsystemen von Bedeutung ist. Die Relativgeschwindigkeit ist jedoch für beide IS identisch, und es kann kein „bewegtes“ und „unbewegtes“ IS geben – beide sind absolut gleichberechtigt, das ist doch das Relativitätsprinzip, das ist doch der Sinn der SRT.

In Ermangelung solcher elementaren Physikkenntnisse schrieb er: „sind in den Punkten A und B von K ruhende, im ruhenden System betrachtet, synchron gehende Uhren vorhanden, und bewegt man die Uhr A mit der Geschwindigkeit v auf der Verbindungslinie nach B, so gehen nach Ankunft dieser Uhr in B die beiden Uhren nicht mehr synchron, sondern die von A nach B bewegte Uhr geht gegenüber der von Anfang an in B befindlichen um ½ tv²/V² Sek. (bis auf Größen vierter und höherer Ordnung) nach, wenn t die Zeit ist, welche die Uhr von A nach B braucht.
Man sieht sofort, dass dies Resultat auch noch dann gilt, wenn die Uhr in einer beliebigen polygonalen Linie sich von A nach B bewegt, und zwar auch dann, wenn die Punkte A und B zusammenfallen. .... so erhält man den Satz: Befinden sich in A zwei synchron gehende Uhren und bewegt man die eine derselben auf einer geschlossenen Kurve mit konstanter Geschwindigkeit, bis sie wieder nach A zurückkommt, was t Sek. dauern möge, so geht die letztere Uhr bei ihrer Ankunft in A gegenüber der unbewegt gebliebenen um ½ t(v/V)² nach.“
Wundern Sie sich nicht, dass Einstein hier „geht“ und „anzeigt“ mehrmals verwechselt, er nahm alles nicht so genau.
So wurde die Grundlage des Zwillingsparadoxons gelegt.
Erst 1918 gab Einstein in „Dialog über Einwände gegen die Relativitätstheorie“ seinen Fehler indirekt zu und versuchte auf Umwege eine reale Zeitdilatation nur während Beschleunigungsvorgänge aufrechtzuerhalten.

Wie sieht aber die Minkowski-SRT (Weltpostulat 1908) aus: Zuerst möchte ich hier nochmals betonen, dass Aussagen wie: „Einstein habe 1905 Zeit und Raum relativiert“ nicht der Wahrheit entsprechen. Nur die Zeit (Uhrzeit, Uhranzeigen, um genau zu sein) war es, erst Minkowski relativierte den Raum - „nur als Verwegenheit mathematischer Kultur“. In seiner Theorie existieren keine Uhren, die durch Einsteins-Synchronisationsmethode „so gerichtet“ werden – alle Uhren laufen dort synchron und entsprechen der Grundgedanke der SRT, nämlich, alle physikalischen Prozesse verlaufen in jedem Inertialsystem identisch. Bei Minkowski ist die Raumkrümmung zwischen den zueinander bewegten Beobachter der Grund für die „verfälschten“ Wahrnehmungen bezüglich Uhrzeit und Längen. Diese Raumkrümmung ist absolut symmetrisch für beide Beobachter und die physikalische Begründung nach Minkowski lautet: „als Geschenk von oben, als Begleitumstand des Umstandes der Bewegung“. Eine physikalische Begründung für die angenommene Konstanz der Lichtgeschwindigkeit ist bei ihm, genauso wie bei Einstein, nicht zu finden.
So umgeht er den real gedachten Maxwell-Lorentz- und spukhaften Einsteins-Äther. Bei Minkowski sind also die Zeitdilatation und Längenkontraktion nur Scheinvorgänge aus der Sicht des fremden IS. Im Einsteins-SRT ist das auch der Fall, was aber Albert nicht ganz mitbekommen hat. Sommerfeld wunderte sich über die Aussagen von Einstein und meinte: „Das Nachgehen der bewegten Uhr zeigt also nicht eigentlich „Bewegung“, sondern „beschleunigte Bewegung“ an.“

Ein Grundsatz der Spezielle Relativitätstheorie ist: Wird die Invarianz der Lichtgeschwindigkeit als real postuliert, dann sind die Längenkontraktion und Zeitdilatation automatisch nur scheinbar und umgekehrt – sind die LK und ZD als real zu betrachten, dann wird die Invarianz der LG automatisch scheinbar.

X. Wie bei der eingehenden Untersuchung des Zwillingsparadoxons in Minkowski-Diagrammen und Überprüfung nach den Grundsätzen der Relativitätstheorie und Lorentztransformation, besonders unter Kapitel IV - Längenkontraktion, festgestellt haben, befindet sich der Umkehrpunkt aus Sicht des Reisenden wo anders, als aus der Sicht des Erdlings. Das Zwillingsparadoxon erwies sich als nicht existent. Es entsteht jedoch ein weitaus bedeutendes Problem der SRT, das wir Phantomparadox nennen können.
Betrachten wir eine realistische Situation, wo die Rakette nur vorbei an den Zielplanet fliegt und sich weiter entfernt. So vermeiden wir das Durcheinander mit mehrfach gesehenen Zeiten zu gleichem Zeitpunkt. Unter Einbehaltung der Invarianz der Lichtgeschwindigkeit ergibt sich folgendes Bild:
Würde der Erdling bei 2J irdischer Zeit ein Licht-, Funksignal zu der Rakete und dem Zielplanet senden, wird er nach genau 6J das Signal von beiden, Rakete und Zielplanet bekommen. Nach seiner Rechnung befanden sich beide Objekte bei 5J irdischer Zeit genau auf 3LJ entfernt und entsprechend am gleichen Ort. Der Zeitstempel aus der Rakete würde 4J lauten und der Zeitstempel aus dem Zielplanet 5J. Soweit, so gut, nun, würde die Rakete auch einen Raumlage-, Raumkoordinaten-Stempel mitsenden, müsste er 2,4LJ von der Erde und 0,6LJ vom Zielplanet entfernt lauten. Die Nachricht aus dem Zielplanet müsste jedoch auch bestätigen, dass das Raumschiff sich unmittelbar am Ort befindet.

Die Aussagen der Beteiligte:
Erde: Zu meiner Zeit 5J befand sich das Raumschiff am Ziel, obwohl seine Uhr 4J zeigte.
Zielplanet: Meine Zeit ist 5J und das Raumschiff ist gerade eingetroffen, wir können es sehen und seine Uhr zeigt 5J.
Raumschiff: Meine Zeit ist 4J. Ich sehe den Zielplanet überhaupt nicht und nach meinen Messungen und Bordanzeigen befindet er sich auf noch 0,6LJ und 1J-Reisezeit von mir entfernt.

Folgerung: Aus einer Rakete sind es zwei geworden, welche davon ist nur ein Phantom? Oder, wenn jemandem lieber ist, können wir auch so umdeuten - es ist nur eine Rakete, aber aus dem Zielplanet sind es zwei geworden, oder es ist nur eine Rakette, ein Zielplanet, aber aus der Raketenuhr und -Maßstab sind es je zwei geworden.

Somit ist, meiner Meinung nach, erwiesen, dass die SRT nur falsche Messergebnisse liefern kann.

Wer kann einen Fehler in den obigen Betrachtungen finden?

Zitate und sinngemäße Wiederdarstellungen dürfen nur mit Quellenangabe veröffentlicht werden!

Literaturverzeichnis:
A. Einstein - „Zur Elektrodynamik bewegter Körper“ - Ann. d. Physik 17 (1905) S.891
A. Einstein - „Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen“ - Jahrbuch d. Radioaktivität u. Elektronik IV (1907) S. 411
H.A. Lorentz, A. Einstein, H. Minkowski, A. Sommerfeld - „Das Relativitätsprinzip - Monographien“ - Herausgeber: Otto Blumenthal - Verlag B.G. Teubner (1913) -
A. Einstein - „Dialog über Einwände gegen die Relativitätstheorie“ - Die Naturwissenschaften, Heft 48 (1918) S. 697

<< Home